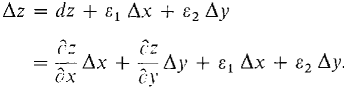| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Partial Differentiation Total Differentials and Tangent Planes Corollary 1 |
|
 Search the VIAS Library | Index
|
  |
Corollary 1
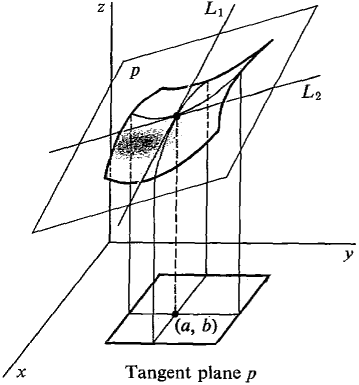
The following corollary is analogous to the theorem that a differentiable function of one variable is continuous. COROLLARY 1 If a function z = f(x, y) is smooth at (a, b) then it is continuous at (a, b). PROOF Let (x, y) be infinitely close to (a, b) and let Δx = x - a, Δy = y - b. Then Since Δx and Δy are infinitesimal, Δz is infinitesimal, so f(x, y) ≈ f(a, b). Some examples of what can happen when the function is not smooth are given in the problem set. If a function z = f(x, y) is smooth at (a, b), the curve z = f(x, b) has a tangent line L, on the plane y = b, and the curve z = f(a, y) has a tangent line L2 on the plane x = a. L1 has the equation z - f(a, b) = fx(a, b)(x - a) and L2 has the equation z - f(a, b) = fy(a, b)(y - b). The plane determined by the lines L1 and L2 is called the tangent plane. It has the equation z - f(a, b) = fx(a, b)(x -a) + fy(a, b)(y - b), because the graph p of this equation is a plane and intersects the plane y = b in Lx and the plane x = a in L2 (Figure 11.4.4).
Figure 11.4.4
|
|
| Home Partial Differentiation Total Differentials and Tangent Planes Corollary 1 |
|
Last Update: 2010-11-25