| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Partial Differentiation Total Differentials and Tangent Planes The Tangent Plane |
|
 Search the VIAS Library | Index
|
  |
The Tangent Plane
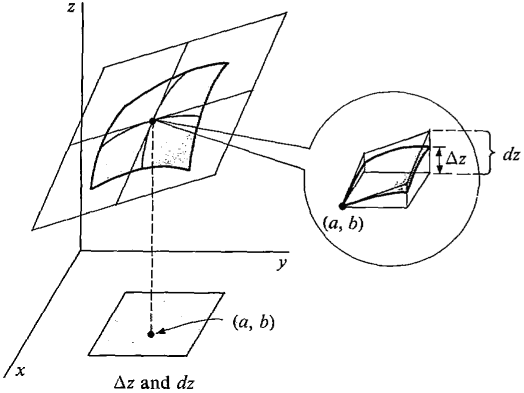
DEFINITION The tangent plane of a smooth function z = f(x, y) at (a, b) is the plane with the equation z - f(a, b) = fx(a, b)(x - a)+ fy(a, b)(y - b). If we set x = a and y = b in this equation we get z = f(a, b). If we set x - a = dx and y - b = dy we get z - f(a, b) = dz. Therefore: The tangent plane touches the surface at (a, b). Δz = change in z on the surface. dz = change in z on the tangent plane. Figure 11.4.5 shows Δz and dz.
Figure 11.4.5
|
|
| Home Partial Differentiation Total Differentials and Tangent Planes The Tangent Plane |
|
Last Update: 2010-11-25