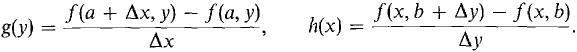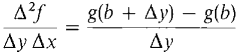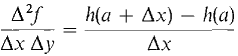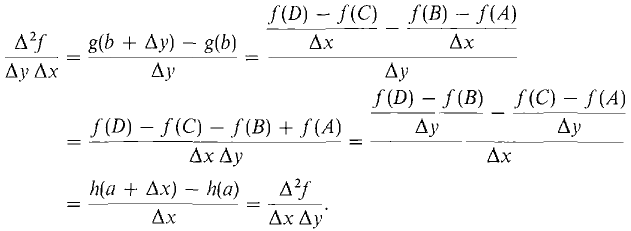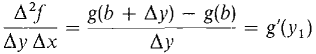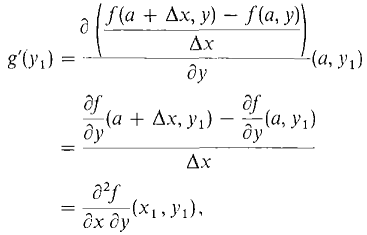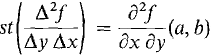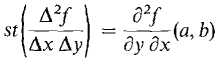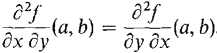PROOF OF THEOREM 1

The plan is to prove a corresponding result for average slopes and then use the Mean Value Theorem, which states that the average slope of a function on an interval is equal to the slope at some point in the interval.

Let Δx and A3¹ be positive infinitesimals. We hold Δx and Δy fixed. The first and second partial derivatives of f(x, y) exist for (x, y) in the rectangle

a ≤ x ≤ a + Δx, b ≤ y ≤ b + Δy.

We shall use the following notation for average slopes in the x and y directions:

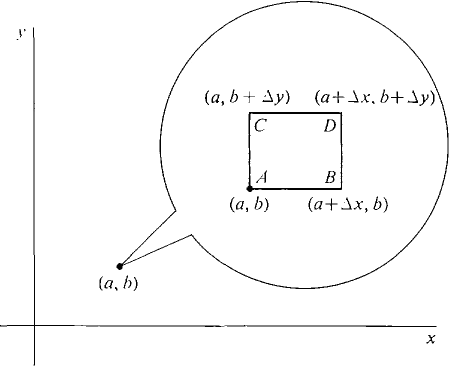
Label the corners of the rectangle A, B, C, and D as in Figure 11.8.1.

Figure 11.8.1

We first show that the following two quantities are equal:

A²f/Δy Δx is the average slope in the y direction of the average slope in the x direction of f

By the Mean Value Theorem,

where b ≤ y_l ≤ b + Δy. Using the Mean Value Theorem again,

where a ≤ x_l ≤ a + Δx. Since ∂²f/∂x ∂y is continuous at (a, b),

A similar computation gives

Therefore