| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Higher Partial Derivatives Higher Partial Derivatives  Theorem 1: Equality of Mixed Partials Theorem 1: Equality of Mixed Partials |
|||||






|
|||||
Theorem 1: Equality of Mixed Partials
THEOREM 1 (Equality of Mixed Partials) Suppose that the first and second partial derivatives of z = f(x, y) are continuous at (a, b). Then at (a, b),
Discusson This is a surprising theorem. ∂2z/∂y ∂x is the rate of change with respect to y of the slope ∂z/∂x, while ∂2z/∂x ∂y is the rate of change with respect to x of the slope ∂z/∂y. There is no simple intuitive way to see that these should be equal. As a matter of fact, there are functions f(x, y) whose mixed second partial derivatives exist but are not equal. One such example is the function
We have left the computation of the second partials of f(x,y) as a problem. It turns out that at (0, 0),
How can this be in view of Theorem 1? The answer is that in this example the second partial derivatives exist but are not continuous at (0, 0), so the theorem does not apply. We shall only rarely encounter functions whose second partial derivatives are not continuous, so in all ordinary problems it is true that the mixed partials are equal. We shall prove the theorem later. We now turn to some applications. Our first application concerns mixed third partial derivatives. If the third partial derivatives of z = f(x, y) are continuous, then
so we write
and we write We prove the first equation as an illustration.
If a function has continuous second partial derivatives we may apply the Chain Rule to the first partial derivatives. For one independent variable,
By holding one variable fixed in Theorem 1, we get equalities of mixed partials for functions of three or more variables. COROLLARY (Equality of Mixed Partials, Three Variables) Suppose that the first and second pairtial derivatives of w = f(x, y, z) are continuous at (a, b, c). Then at (a, b, c),
|
|||||
Home  Partial Differentiation Partial Differentiation  Higher Partial Derivatives Higher Partial Derivatives  Theorem 1: Equality of Mixed Partials Theorem 1: Equality of Mixed Partials |
|||||
Last Update: 2006-11-05






 for each of them. Similarly,
for each of them. Similarly,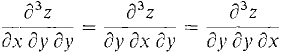
 for each of them.
for each of them.



