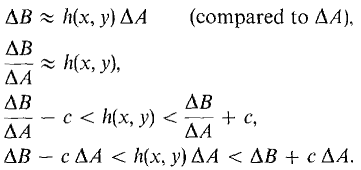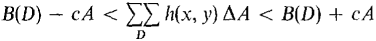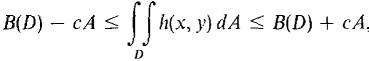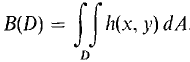| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Multiple Integrals Infinite Sum Theorem and Volume Infinite Sum Theorem Proof |
|
 Search the VIAS Library | Index
|
  |
Proof
PROOF WHEN D IS A RECTANGLE Choose positive infinitesimal Δx and Δy and partition D into elements of area ΔD (Figure 12.3.2). Since B has the Addition Property, B(D) is the sum of the ΔB's. Let c be any positive real number. For each ΔD we have
Letting A be the area of D and adding up,
Taking standard parts,
so
Figure 12.3.2 The proof in the general case is similar except that some of the elements of area ΔD will overlap the boundary of D and thus be only partly within D. (See Figure 12.3.3.) The method of proof is to change D to include all instead of part of each ΔZ), use hypothesis (ii) to show that the new B(D) is infinitely close to the old one, and then show as above that the new B(D) is infinitely close to the double integral ∫∫D h(x,y) dA.
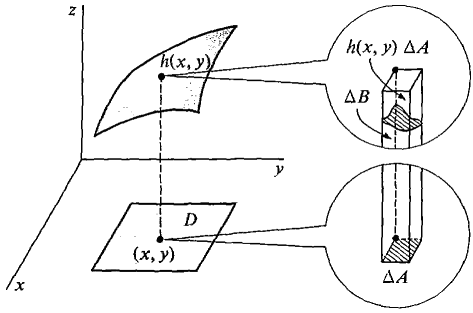
Figure 12.3.3 In most applications of the Infinite Sum Theorem, hypotheses (i) and (ii) are automatic. To get a formula for B(D) in practice, we take an element of area ΔD and find an h(x, y) such that ΔB ≈ h(x, y) ΔA (compared to ΔA).
|
|
| Home Multiple Integrals Infinite Sum Theorem and Volume Infinite Sum Theorem Proof |
|
Last Update: 2010-11-25