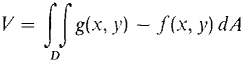The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Multiple Integrals Infinite Sum Theorem and Volume Volume Between Two Surfaces
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Volume Between Two Surfaces

Our first application is to the volume between two surfaces.

DEFINITION

Let

f(x, y) ≤ g(x, y)

for (x, y) in D and let E be the set of all points in space such that

(x, y) is in D, f(x, y) ≤ z ≤ g(x, y).

The volume of E is

12_multiple_integrals-162.gif

V is called the volume over D between the surfaces z = f(x, y) and z = g(x, y) (Figure 12.3.4).

12_multiple_integrals-163.gif

Figure 12.3.4: Volume between two surfaces

JUSTIFICATION

The part ΔE of the solid E over an element of area ΔD is a rectangular solid with base ΔA and height g(x, y) - f(x, y), except that the top and bottom surfaces are curved (Figure 12.3.5). Therefore the volume of ΔE is

ΔV ≈ (g(x, y) - f(x, y)) ΔA (compared to ΔA).

By the Infinite Sum Theorem,

12_multiple_integrals-164.gif

12_multiple_integrals-165.gif

Figure 12.3.5

Example 1
Example 2
Example 3

Home Multiple Integrals Infinite Sum Theorem and Volume Volume Between Two Surfaces

Last Update: 2010-11-25