| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Infinite Sum Theorem and Volume Infinite Sum Theorem and Volume  Examples Examples  Example 3 Example 3 |
|||||||






|
|||||||
Example 3
Find the volume of the solid bounded by the plane z = 2y and the paraboloid z = 1 - 2x2 - y2.
Figure 12.3.8 (a): Surfaces
Figure 12.3.8. (b): Region D
Figure 12.3.9 Answer: V = √2π.
|
|||||||
Home  Multiple Integrals Multiple Integrals  Infinite Sum Theorem and Volume Infinite Sum Theorem and Volume  Examples Examples  Example 3 Example 3 |
|||||||
Last Update: 2006-11-15




 Therefore D is the region
Therefore D is the region ≤ y ≤ -1 +
≤ y ≤ -1 + 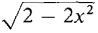

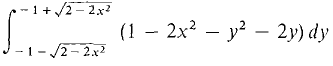
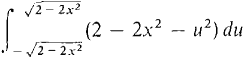 =
=

 = cos θ, dx = cos θ dθ (Figure 12.3.9).
= cos θ, dx = cos θ dθ (Figure 12.3.9).
