| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Double Integrals in Polar Coordinates Double Integrals in Polar Coordinates  Polar Regions Polar Regions |
|






|
|
Double Integrals in Polar Coordinates
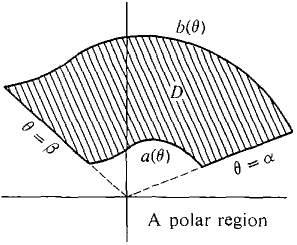
A point with polar coordinates (θ, r) has rectangular coordinates (x, y) = (r cos θ, r sin θ). DEFINITION A polar region is a region D in the (x, y) plane given by polar coordinate inequalities α ≤ 0 ≤ β, a(θ) ≤ r ≤ b(θ), where a(θ) and b(θ) are continuous. To avoid overlaps, we also require that for all (0, r) in D, 0 ≤0 ≤2π and 0 ≤ r. The last requirement means that the limits α and β are between 0 and 2π, while the limits a(θ) and b(θ) are ≥ 0. Figure 12.5.1 shows a polar region.
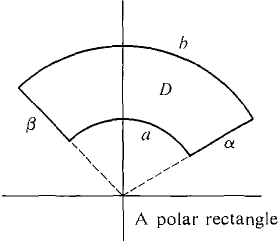
Figure 12.5.1 The simplest polar regions are the polar rectangles α ≤ θ ≤β, a ≤ r ≤ b. We see in Figure 12.5.2 that the θ boundaries are radii and the r boundaries are circular arcs.
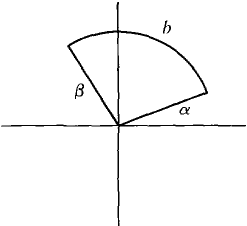
Figure 12.5.2 The polar rectangle α≤θ ≤ β, 0≤ r ≤ b is a sector of a circle of radius b (Figure 12.5.3(a)).
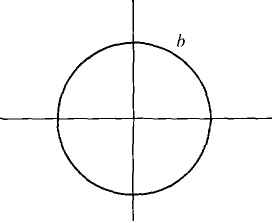
Figure 12.5.3 (a) sector: α ≤ θ ≤ β, 0≤ r ≤b The polar rectangle 0 ≤ θ ≤ 2π, 0 ≤ r ≤ b is a whole circle of radius b (Figure 12.5.3(b)).
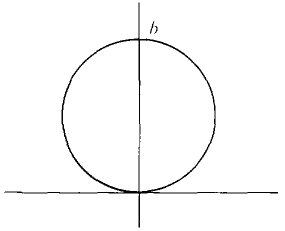
Figure 12.5.3 (b) circle: 0 ≤ θ ≤ 2π, 0 ≤ r ≤ b Less trivial examples of polar regions are the circle with diameter from (0,0) to (0, b), 0 ≤ θ ≤π, 0 ≤ r ≤ b sin θ, and the cardioid 0 ≤ θ ≤ 2π, 0 ≤ r ≤ 1 + cos θ. Both of these regions are shown in Figure 12.5.4.
Figure 12.5.4 (a) circle: 0 ≤ θ ≤ ir, 0 ≤ r ≤ b sin θ (b) cardioid: 0 ≤ θ ≤ 2π, 0 ≤ r ≤ 1 + cos θ
We shall use the Infinite Sum Theorem to get a formula for the double integral over a polar region. In the proof we take for ΔD an infinitely small polar rectangle.
|
|
Home  Multiple Integrals Multiple Integrals  Double Integrals in Polar Coordinates Double Integrals in Polar Coordinates  Polar Regions Polar Regions |
|
Last Update: 2010-11-25