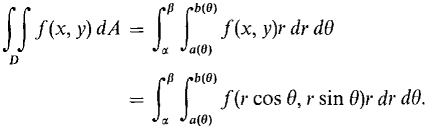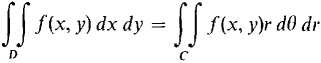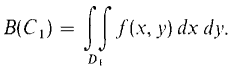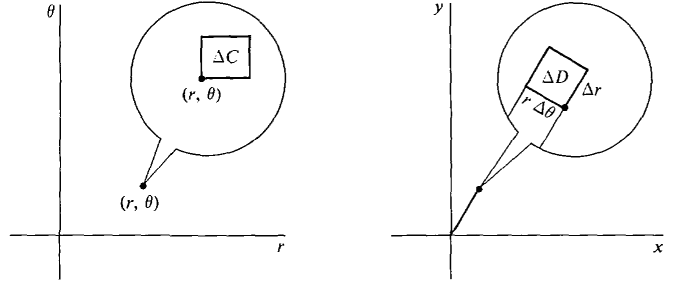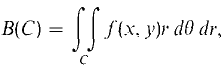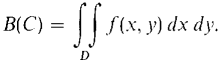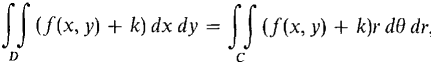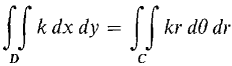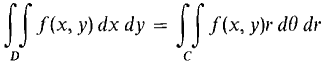Polar Integration Formula

Let D be the polar region

α ≤ θ ≤ β, a(θ) ≤ r ≤ b(θ).

The double integral of f(x, y) over D is

Notice that in the iterated integral for a polar region we do not integrate f(x, y) but the product of f(x, y) and r. Intuitively, the extra r comes from the fact that a polar element of area is almost a rectangle of area r Δθ Δr (see Figure 12.5.6(b)).

Figure 12.5.6 (b) Exaggerated scale

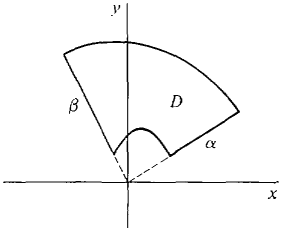
PROOF

We shall work with the rectangular (θ, r) plane. Let C be the region in the (θ, r) plane given by the inequalities

a ≤ θ ≤ β, a(θ) ≤ r ≤ b(θ).

Figure 12.5.5

Thus C has the same inequalities as D but they refer to the (θ, r) plane instead of the (x,y) plane. D and C are shown in Figure 12.5.5.

We must prove that

Our plan is to use the Infinite Sum Theorem in the (θ, r) plane. Assume first that f(x, y) > 0 for all (x, y) in D.

For any (θ, r) region C₁ corresponding to a polar region D_l in the (x, y) plane, let

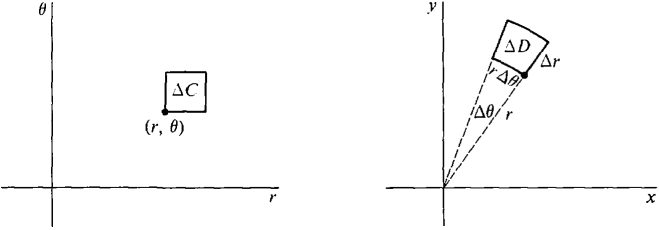
Then B has the Addition Property and is always ≥ 0. Consider an element of area AC in the (θ, r) plane with area Δθ Δr. ΔC corresponds to a polar rectangle ΔD in the (x, y) plane. As we can see from Figure 12.5.6, ΔD is almost a rectangle with sides r Δθ and Δy and area r Δθ Δr.

Figure 12.5.6 (a) Under microscopes

The volume over ΔD is almost a rectangular solid with base of area r Δθ Δr and height

f(x, y) = f(r cos θ, r sin θ).

Therefore B(ΔC) ≈ f(x, y)r Δθ Δr (compared to Δθ Δr). By the Infinite Sum Theorem

and by definition

Finally we consider the case where f(x, y) is not always positive. Pick a real constant k > 0 such that f(x, y) + k is always positive for (x, y) in D. By the above proof,

When we use the Sum Rule and subtract the second equation from the first, we get

In a double integration problem where the region D is a circle or a sector of a circle, it is usually best to take the center as the origin and represent D as a polar rectangle.