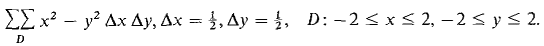Extra Problems for Chapter 12

1            Compute the Riemann sum

2            Compute the Riemann sum

3            Evaluate

4            Evaluate

5            Evaluate

6            Evaluate

7            Find the volume of the solid over the region - 1 ≤ x ≤ 1, 0 ≤ y ≤ 1 - x² and between the surfaces z = 0, z = 1 - y.

8            Find the volume of the solid over the region x² + y¹ = 4 and between the surfaces z = 0 and z = y² + x + 2.

9            Find the volume of the solid 1 ≤ x ≤ 2, 0 ≤ y ≤ in x, y/x ≤ z ≤ 1/x.

10            Find the volume of the solid x² + y² ≤ 1, x²y³ ≤ z ≤ 1.

11             Find the volume of the solid bounded by the planes

x = 1, x = y, z = x + y, z = x + 2,

12            Find the volume of the solid bounded by the cylinders

x² + y² = 1, x² + z² = 1.

13            Find the mass, center of mass, and moment of inertia about the origin of the plane

object

0 ≤ x ≤ π, 0 ≤ y ≤ sin x, ρ(x, y) = k.

14            Find the mass, center of mass, and moment of inertia about the origin of the plane object

0≤x≤l, x≤y≤l, ρ(x, y) = x²y.

15            A circular disc filling the region x² + y² ≤ r² has density ρ(x, y) = y². Find the mass, center of mass, and moment of inertia about the origin.

16            A semicircular object on the region

has density ρ(x, y) = y. Find the work required to stand the object up on its flat side.

17            Using polar coordinates, find the volume of the solid

x² + y² ≤ 9, y ≤ z ≤ x + 5.

18            Find the volume of the solid over the region 0 ≤ r ≤ 3 + cos θ between the plane z = 0 and the cone z = r.

19            Find the volume of the solid over the circle 0 ≤ r ≤ a between the plane z = 0 and the surface z = 1/r.

20            Find the mass and the moment of inertia about the origin of a semicircular object 0 ≤ r ≤ l, 0 ≤ θ ≤ 7π whose density is ρ(r, θ) = rθ.

21            A plane object covers the circle 0 ≤ r ≤ a and its density depends only on the distance r from the center, ρ(r, θ) = f(r). Show that the center of mass is at the origin.

22            Evaluate

23            Evaluate

24            Evaluate the triple integral

25            An object has constant density k in the region

Find its center of mass and its moments of inertia about the coordinate axes.

26            Use cylindrical coordinates to evaluate ∫∫∫_E z dV, where E is the region inside the cylinder x² + y² = 1 which is above the plane z = 0 and within the sphere x² + y² + z² = 9.

27            An object of constant density k has the shape of a parabolic bowl

Find its center of mass and its moment of inertia about the z-axis.

28             Use spherical coordinates to evaluate the integral

E is the spherical octant

29            A spherical shell a ≤ ρ ≤ b has density equal to the distance from the center. Find its mass and its moment of inertia about a diameter.

30            Prove that the double Riemann sum ∑∑_D f(x, y) dx dy is finite whenever f(x,y) is continuous, D is a closed region, and dx, dy are positive infinitesimals.

31             Suppose a plane object is symmetric about the x-axis, that is, it covers a region D of the form

and has density ρ(x, y) = ρ(x, -y). Prove that the center of mass is on the x-axis.

32            The moment of inertia about the x-axis of a point in the plane of mass m is I_x = my². Use the Infinite Sum Theorem to show that the moment of inertia about the x-axis of a plane object with density ρ(x, y) in the region D is I_x = ∫∫_D ρ(x, y)y² dA.

33            The kinetic energy of a point of mass m moving at speed v is KE = ½mv². A rigid object of density ρ(x, y) in the plane region D is rotating about the origin with angular velocity ω (so a point at distance d from the origin has speed ωd). Use the Infinite Sum Theorem to show that the kinetic energy of the object is

.34           Suppose a plane object is symmetric about the origin; that is, it fills a polar region

0 ≤ r ≤ g(θ), -π ≤ d ≤ π, such that g(θ ± π) = g(θ), and its density has the property ρ(r, θ) = ρ(r, θ ± π). Show that the center of mass is at the origin.

35           Use the Infinite Sum Theorem to show that if D is a polar region of the form a ≤ r ≤ b,

α(r) ≤ θ ≤ β(r), then