| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Directional Derivatives and Gradients Directional Derivatives and Gradients  The Unit Vector The Unit Vector |
|






|
|
The Unit Vector
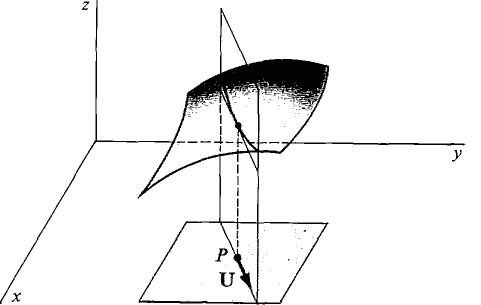
The partial derivatives ∂z/∂x and ∂z/∂y are the rates of change of z = f(x, y) as the point (x, y) moves in the direction of the x-axis and the y-axis. We now consider the rate of change of z as the point (x, y) moves in other directions. Let P(a, b) be a point in the (x, y) plane and let U = cos αi + sin αj be a unit vector, a is the angle from the x-axis to U (see Figure 13.1.1). The line through P with direction vector U has the vector equation X = P + tU or in parametric form, (1) x = a + t cos α,
Figure 13.1.1 The unit vector At t = 0 we have x = a and y = b. If we intersect the surface z = f(x, y) with the vertical plane through the line (Equation 1), we obtain the curve z = f(a + t cos α, b + t sin α) = F(t). The slope dz/dt = F'(0) of this curve at f = 0 is called the slope or derivative of f in the U direction and is written fU(a, b) (Figure 13.1.2).
Figure 13.1.2: The directional derivative Here is the precise definition. DEFINITION Given a function z = f(x, y) and a unit vector U = cos αi + sin αj, the derivative of f in the U direction is the limit
fU(a, b) is called a directional derivative of f at (a, b). The partial derivatives of f(x, y) are equal to the derivatives of f(x, y) in the i and j directions: 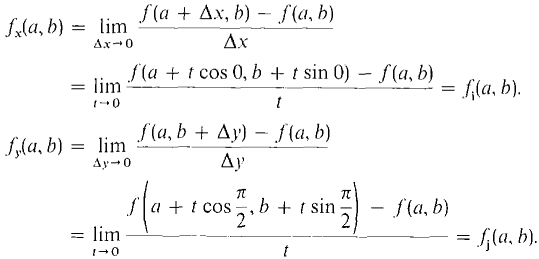
|
|
Home  Vector Calculus Vector Calculus  Directional Derivatives and Gradients Directional Derivatives and Gradients  The Unit Vector The Unit Vector |
|
Last Update: 2006-11-17