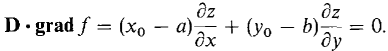The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Vector Calculus Directional Derivatives and Gradients Corollaries
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Corollaries

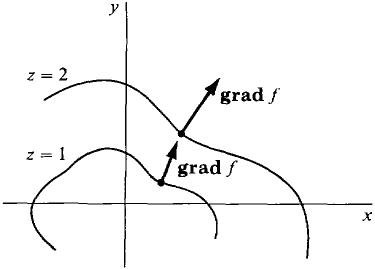
We can use Theorem 1 to give a geometric interpretation of the gradient vector. Let us assume that f(x, y) is smooth at a point (a, b), and see what happens to the directional derivatives fU(a, b) as the unit vector U varies. If both partial derivatives fx(a, b) and fy(a, b) are zero, then the gradient vector and hence all the directional derivatives are zero. Suppose the partial derivatives are not both zero, whence grad f ≠ 0. Then

fU = U · grad f = |grad f| cos θ

where θ is the angle between U and grad f. Therefore fU is a maximum when cos θ = 1 and θ = 0, a minimum when cos θ = - 1 and θ = π, and zero when cos θ = 0 and θ = π/2. We have proved the following corollary.

COROLLARY 1

Suppose z = f(x, y) is smooth and grad f ≠ 0 at (a, b). Then the length of grad f is the largest directional derivative of f, and the direction of grad f is the direction of the largest directional derivative of f.

On a surface z = f(x, y), the direction of the gradient vector is called the direction of steepest ascent, and the direction opposite the gradient vector is called the direction of steepest descent (Figure 13.1.4).

13_vector_calculus-12.gif

Figure 13.1.4

COROLLARY 2

Suppose z = f(x, y) is smooth and ∂z/∂y ≠ 0 at (a, b). Then grad f is normal (perpendicular) to the level curve at (a, b). That is, grad f is perpendicular to the tangent line of the level curve (Figure 13.1.5).

 

Figure 13.1.513_vector_calculus-13.gif

PROOF

By the Implicit Function Theorem, the level curve

f(x,y) - f(a,b) = 0

has the tangent line

13_vector_calculus-14.gif

(a, b) is on this line. Let (x0, y0) be any other point on the line. Then

D = (x0 - a)i + (y0 - b)j

is a direction vector of the line, and

13_vector_calculus-15.gif

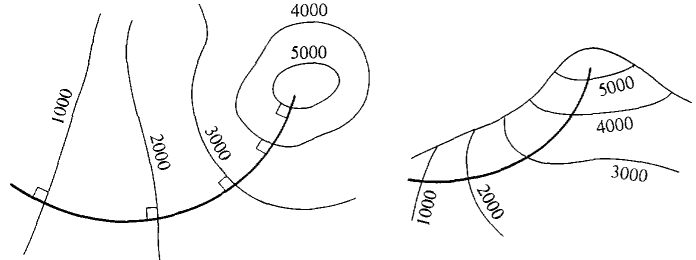
Thus grad f is perpendicular to the direction vector D.

Water always flows down a hill in the direction of steepest descent. Thus on a topographic map, the course of a river must always be perpendicular to the level curves, as in Figure 13.1.6.

13_vector_calculus-16.gif

Figure 13.1.6
Home Vector Calculus Directional Derivatives and Gradients Corollaries

Last Update: 2006-11-25