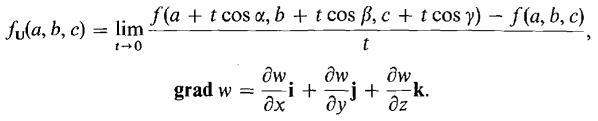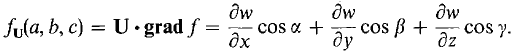The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Vector Calculus Directional Derivatives and Gradients Directional Derivatives and Gradients (Three Variables)
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Directional Derivatives and Gradients (Three Variables)

Directional derivatives and gradients for functions of three variables are similar to the case of two variables.

DEFINITION

Given a real function

w = f(x, y, z)

and a unit vector

U = cos αi + cos βj + cos γk

in space, the derivative of f in the direction U and the gradient of f at (a, b, c) are defined as follows.

13_vector_calculus-20.gif

THEOREM 2

Suppose w = f(x, y, z) is smooth at (a, b, c). Then for any unit vector

U = cos αi + cos βj + cos γk,

the directional derivative fU(a, b, c) exists and

13_vector_calculus-21.gif

Corollaries 1 and 2 also hold for functions of three variables. In Corollary 2, grad f is normal to the tangent plane of the level surface f(x, y, z) - f(a, b, c) = 0 at (a, b, c).
Home Vector Calculus Directional Derivatives and Gradients Directional Derivatives and Gradients (Three Variables)

Last Update: 2006-11-25