| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Surface Area and Surface Integrals Surface Area and Surface Integrals  Problems Problems |
|






|
|
Problems
1 Find the area of the triangle cut from the plane x + 2y + 4z = 10 by the coordinate planes. 2 Find the area cut from the plane 2x + 4y + z = 0 by the cylinder x2 + y2 = 1. 3 Find the area of the surface of the paraboloid z = x2 + y2 below the plane z = 1. 4 Find the area of the surface of the cone 5 Find the surface area of the part of the sphere x2 + y2 + z2 = a2 which lies in the first octant; i.e., x ≥ 0, y ≥ 0, z ≥ 0. 6 Find the surface area of the part of the sphere x2 + y2 + z2 = a2 which is above the circle x2 + y2 ≤ b2 (b ≤ a). 7 Find the surface area cut from the hyperboloid z = x2 - y2 by the cylinder x2 + y2 = a2. 8 Find the area cut from the surface z = xyby the cylinder x2 + y2 = a2. 9 Find the surface area of the part of the sphere r2 + z2 = a2 above the circle r = a cos θ. 10 Find the surface area of the part of the cone z = cr above the circle r = a cos θ. 11 Find the area of the part of the plane z = ax + by + c over a region D of area A. 12 Find the surface area of the part of the cone 13 Find the surface area of the part of the cylinder x2 + z2 = a2 cut out by the cylinder x2 + y2 ≤ a2. 14 Find the surface area of the part of the cylinder x2 + z2 = a2 above and below the square -b ≤ x ≤ b, -b ≤ y ≤ b (b ≤ a). 15 Evaluate the surface integral
where S is the surface z = x2 + y2, -1 ≤ x ≤ 1, - 1 ≤ y ≤ 1, oriented with the top side positive. 16 Evaluate the surface integral
where S is the surface z = 3x - 5y over the rectangle 1 ≤ x ≤ 2, 0 ≤ y ≤ 2, oriented with the top side positive. 17 Evaluate the surface integral where S is the surface z = 1 - x2 - y2, x2 + y2 ≤ 1, oriented with the top side positive. 18 Evaluate the surface integral
where S is the surface z = x + y2 + 2, 0 ≤ x ≤ 1, x ≤ y ≤ 1, oriented with the top side positive. 19 Evaluate the surface integral
where S is the surface z = xy, 0 ≤ x ≤ 1, - ,x ≤ y ≤ x, oriented with the top side positive. 20 Evaluate the surface integral
where S is the surface positive (b < a). 21 Show that if S is a horizontal surface z = c over a region D, oriented with the top side positive, then the surface integral over S is
|
|
Home  Vector Calculus Vector Calculus  Surface Area and Surface Integrals Surface Area and Surface Integrals  Problems Problems |
|
Last Update: 2006-11-25


 below the plane z = 2.
below the plane z = 2. over a region D of area A.
over a region D of area A.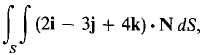
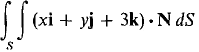

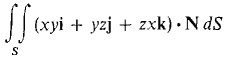

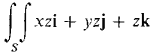
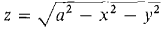 , x2 + y2 ≤ b, oriented with the top side
, x2 + y2 ≤ b, oriented with the top side