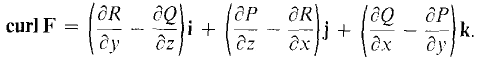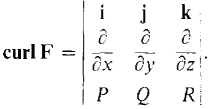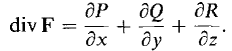| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Theorems of Stokes and Gauss Theorems of Stokes and Gauss  Curl of a Vector Field Curl of a Vector Field |
|






|
|
Curl of a Vector Field
Both Stokes' Theorem and Gauss' Theorem are three-dimensional generalizations of Green's Theorem. To state these theorems we need the notions of curl and divergence in three dimensions. The curl of a vector field in the plane is a scalar field, while the curl of a vector field in space is another vector field. However, the divergence in both cases is scalar. DEFINITION Given a vector field F(x, y, z) = Pi + Qj + Rk in space. The curl of F is the new vector field
This can be remembered by writing the curl as a "determinant"
The divergence of F is the real valued function
|
|
Home  Vector Calculus Vector Calculus  Theorems of Stokes and Gauss Theorems of Stokes and Gauss  Curl of a Vector Field Curl of a Vector Field |
|
Last Update: 2006-11-22