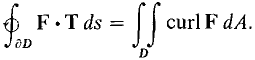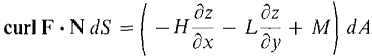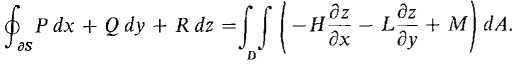Stokes' Theorem

Stokes' Theorem relates a surface integral over S to a line integral over the boundary of S. It corresponds to Green's Theorem in the form

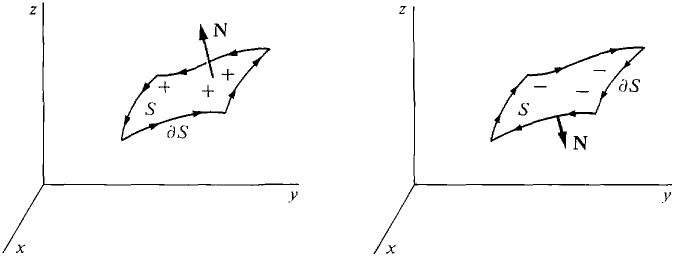
Let S be an oriented surface over a region D. The boundary of S, ∂S, is the simple closed space curve whose direction depends on the orientation of S as shown in Figure 13.6.1.

The notation

denotes the line integral around ∂S in the direction determined by the orientation of S.

Figure 13.6.1 The Boundary of S

To put this equation in scalar form, let

F = Pi + Qj + Rk, curl F = Hi + Lj + Mk.

Then

F · T ds = P dx + Q dy + R dz,

and if S is oriented with the top side positive,

Thus Stokes' Theorem has the scalar form

Stokes' Theorem has two corollaries which are analogous to the Path Independence Theorem.