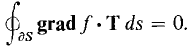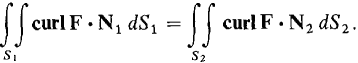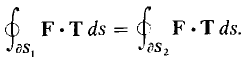The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Vector Calculus Theorems of Stokes and Gauss Corollaries for Stokes' Theorem
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Corollaries for Stokes' Theorem

COROLLARY 1

If f(x, y, z) has continuous second partials, then the line integral of grad f around the boundary of any oriented surface is zero,

13_vector_calculus-320.gif

(See Figure 13.6.3.)

13_vector_calculus-323.gif

Figure 13.6.3 

PROOF

curl(grad f) = 0,

so

13_vector_calculus-321.gif

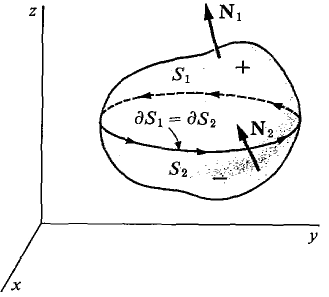
COROLLARY 2

The surface integral of curl F over an oriented surface depends only on the boundary of the surface. That is, if ∂S1 = ∂S2 then

13_vector_calculus-322.gif

(See Figure 13.6.4.)

13_vector_calculus-324.gif

Figure 13.6.4

PROOF

By Stokes' Theorem, both surface integrals are equal to the line integral

13_vector_calculus-325.gif

For fluid flows, Stokes' Theorem states that the circulation of fluid around the boundary of an oriented surface S is equal to the surface integral of the curl over S.

We shall not prove Stokes' Theorem, but will illustrate it in the following examples.
Home Vector Calculus Theorems of Stokes and Gauss Corollaries for Stokes' Theorem

Last Update: 2006-11-22