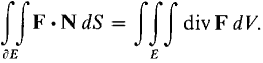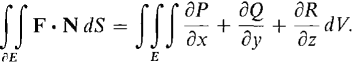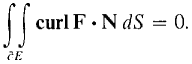| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Vector Calculus Theorems of Stokes and Gauss Gauss' Theorem |
|
 Search the VIAS Library | Index
|
  |
Gauss' Theorem
We are now ready to state Gauss' Theorem. GAUSS' THEOREM Given a vector field F(x, y, z) and a solid region E,
This equation may also be written in the form
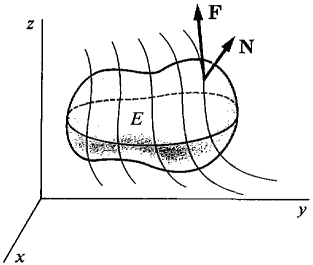
Gauss' Theorem is sometimes called the Divergence Theorem. For fluid flow, Gauss' Theorem states that the outward rate of flow across the boundary of E is equal to the integral of the divergence over E (Figure 13.6.9). As in the two-dimensional case, the divergence is the rate at which the density is decreasing.
Figure 13.6.9 The following corollary is another analogue of the Path Independence Theorem. COROLLARY 3 If F(x, y, z) has continuous second partials, the surface integral of curl F over the boundary of E is zero. In symbols,
PROOF Since div(curl F) = 0,
|
|
| Home Vector Calculus Theorems of Stokes and Gauss Gauss' Theorem |
|
Last Update: 2006-11-22