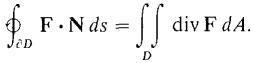| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Theorems of Stokes and Gauss Theorems of Stokes and Gauss  Boundary Of a Solid Region Boundary Of a Solid Region |
|






|
|
Boundary Of a Solid Region
Gauss' Theorem shows a relationship between a triple integral over a region E in space and a surface integral over the boundary of E. It corresponds to Green's Theorem in the form
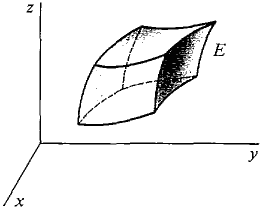
Before stating Gauss' Theorem, we must explain what is meant by the surface integral over the boundary of a solid region E. In general, the boundary of E is made up of six surfaces corresponding to the six faces of a cube (Figure 13.6.7). Sometimes one or more faces will degenerate to a line or a point.
Figure 13.6.7 The top and bottom faces of E are (x, y) surfaces, that is, they are given by equations z = c(x, y). However, the left and right faces of £ are (x, z) surfaces y = b(x, z), while the front and back faces of E are (y, z) surfaces of the form x = a(y, z). Surface integrals over oriented (x, z) and (y, z) surfaces are defined exactly as for (x, y) surfaces except that the variables are interchanged. In the following discussion E is a solid region all of whose faces are smooth surfaces. DEFINITION The boundary of E, ∂E, is the union of the six faces of E oriented so that the outside surfaces are positive. The surface integral of a vector field F(x, y, z) over ∂E,
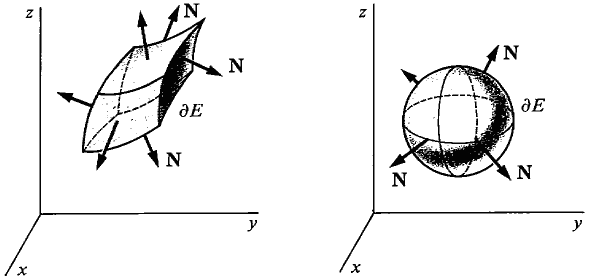
is the sum of the surface integrals of F over the six faces of E. (See Figure 13.6.8.)
Figure 13.6.8: Boundary of E
|
|
Home  Vector Calculus Vector Calculus  Theorems of Stokes and Gauss Theorems of Stokes and Gauss  Boundary Of a Solid Region Boundary Of a Solid Region |
|
Last Update: 2006-11-22