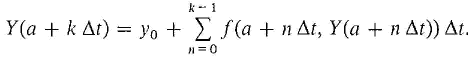Existence And Approximation Of Solutions

This section deals with arbitrary first order differential equations. It is optional and therefore can be omitted if desired. Most first order differential equations cannot be solved explicitly. However, it is possible to approximate a solution by a method similar to the Riemann sum for the definite integral. The Euler approximation

starts by dividing the interval [a, ∞) into small subintervals of length Δt. When Δt is real, it gives an approximate solution that can be computed numerically. When Δt is infinitesimal, it leads to a precise solution and is useful because it shows that a solution exists.

Throughout this section, we shall work with a first order differential equation with an initial value

(1)

y' = f(t,y), y(a) = y₀.

We assume once and for all that f(t, y) is continuous for all t and y.

The graph of Y(t) is the broken line shown in Figure 14.4.1. Each piece has the slope required by the differential equation (1) at the beginning of the subinterval. If Δt is small, then since f(t, y) is continuous, the slope of Y(t) should be close to the correct slope. Thus we would expect Y(t) to be close to a solution of (1).

Figure 14.4.1

The values of Y(t) at the partition points can be computed by an iteration that can easily be carried out on a computer. The first three values are

Given the value Y(t) for a partition point t = a + k Δt, the next value Y(t + Δt) is given by the rule

Y(t + Δt) = Y(t) + f(t, Y(t))Δt.

Using the sigma notation, the (k + 1)^st value of Y(t) can be written as

This equation may also be written in the manner of a Riemann sum with b = a + k Δt:

In the simple case the Euler approximation is just y₀ plus the Riemann sum,

which is approximately equal to y₀ plus the integral