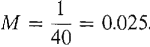Example 3

Find a particular solution of the differential equation

y" + 7y' + 10y = e^3t.

We guess that there is a particular solution that is a constant times e^3t,

y(t) = Me^3t.

The first two derivatives of y(t) are

y'(t) = 3Me^3t,

y"t = 9Me^3t.

Substitute these into the original differential equation.

9Me^3t + 21Me^3t + 10Me^3t = e^3t.

Cancel the e^3t, and solve for the unknown constant M.

9M + 21M + 10M = 1,

The required particular solution is

y(t) = 0.025e^3t.

Here is the rule for guessing a particular solution of the differential equation of the form (1) when the forcing term f(t) is an exponential function f(t) = e^kt. We first should find the roots of the characteristic polynomial az² + bz + c. If k is not a root of the characteristic polynomial, there is a particular solution of the form y(t) = Me^kt (as in Example 3 above). If k is a single root of the characteristic polynomial, there is a particular solution of the form y(t) = Mte^kt. If k is a double root of the characteristic polynomial, there is a particular solution of the form y(t) = Mt²e^kt.