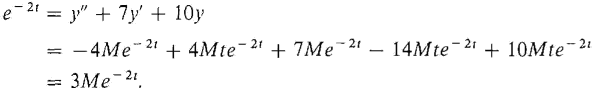Example 4

Find a particular solution of the differential equation

y" + 7y' + 10y = e^-2t.

The characteristic polynomial z² + 7z + 10 has roots -2 and -5. Since - 2 is a single root of the characteristic polynomial, our guess at a particular solution should be

y(t) = Mte^-2t.

The first two derivatives of y(t) are

y'(t) = Me^-2t - 2Mte^-2t, y"(t) = -4Me^-2t + 4Mte^-2t.

Now substitute into the original differential equation.

Then M = 1/3, and the required particular solution is

In this example the simpler guess Le ^-2t would not have worked. The trouble is that Le^-2t is a solution of the corresponding homogeneous equation, so it cannot also be a solution of the original differential equation. To see what happens, let us try to use the method with the guess u(t) = Le^-2t. Computing the first two derivatives and substituting, we get

u'(i) = -2Le^-2t, u"(t) = 4Le^-2t,

e^-2t = u" + 7u' + 10u = 4Le^-2t - 14Le^-2t + 10Le^-2t.

The right side of the above equation adds up to zero, so we cannot solve for the unknown constant L.

In a physical system, the forcing term is often a simple oscillation that can be represented by a function of the form f(t) = G cos (ωt) + H sin (ωt). Here is the rule for guessing a particular solution of the differential equation (1) when the forcing term is f(t) = G cos (ωt) + H sin (ωt). If z = iω is not a root of the characteristic polynomial, then the differential equation will have a particular solution of the form y(t) = K cos (ωt) + L sin (ωt). On the other hand, if z = iω is a root of the characteristic polynomial, then there is a particular solution of the form y(t) = Kt cos (ωt) + Lt sin (ωt).