| The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry. |

|

Home  Coordinate Systems Coordinate Systems  2D 2D  Coordinate Transform Coordinate Transform |
|






|
|
Coordinate Transform
TranslationIn order to translate ("shift") a point P1 to the new position P1' one has to add the translation vector t [tx, ty]:
P1' = P1 + t In terms of individual coordinate values, the new position [x', y'] is calculated as follows:
x' = x + tx
RotationThe rotation of a point around the origin O of the coordinate system does not change the length of the vector OP. Note that positive rotation angles correspond to counter-clockwise rotation:x' = r
ReflectionA reflection flips all the points in the plane over a line, which is called the mirror. Points lying on the mirror line are called invariant points (points that map onto themselves, i.e. P6 in the figure below which is invariant to the reflection about the y-axis). A reflection changes the sense of the figures in the plane.
There are several special cases of 2D reflections:
ScalingEach individual coordinate of each point in the plane is contracted or expanded by the scaling factors Sx and Sy.In the figure below the scaling factors are Sx=2 and Sy=0.5, thus the x-coordinates are multiplied by 2 (expanded), and the y-coordinates are divided by 2 (contracted). Consequently the point P1, for example, is transformed into point P1' by the following equations:
x1' = 2x1
|
|
Home  Coordinate Systems Coordinate Systems  2D 2D  Coordinate Transform Coordinate Transform |
|
Last Update: 2011-01-11



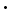 cos(φ1-β)
cos(φ1-β)

