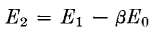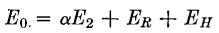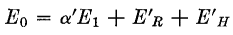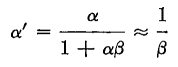Inverse Feedback

If part of the output of an amplifier is fed back to the input in such a way as to oppose it, the ripple, distortion, and frequency response deviations in output are reduced. The amplifier gain is reduced also, but with the availability of high-gain tubes an extra stage or two compensates for the reduction in gain caused by inverse feedback, and the improvement in performance usually justifies it.

Fig. 130. Voltage feedback.

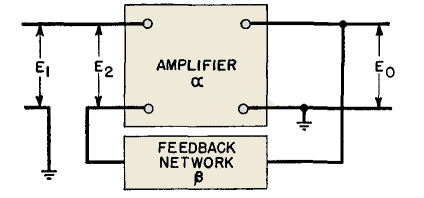
In the amplifier of Fig. 130, a network is shown connected to output voltage E_o; part of this output is fed back so that the input to the amplifier is

[77]

Here β is the portion of E₀ which is fed back. If α is the voltage amplification of the amplifier and E_r and E_H are the ripple and harmonic distortion in the output without feedback, and α', E'_R, and E'_H are the same properties with feedback, the following equations hold, if α, E_R, and E_H are assumed to be independent:

Without feedback,

[78]

With feedback,

[79]

these equations it can be shown that

[80]

[81]

[82]

With high-gain amplifiers and large amounts of feedback, the output ripple and harmonic distortion can be made astonishingly small. Likewise the frequency response can be made flat, even with mediocre transformers. Inverse feedback is not used in class C amplifiers, because the output and input are not linearly related.

Incidental effects in the amplifier, like distributed capacitance and leakage inductance, have to be carefully matched in the inverse feedback network so that the phase shift around the loop does not become too large. If it reaches 180°, feedback is regenerative, so that the amplifier may become an oscillator with a frequency determined by the circuit constants. Nyquist has shown⁽¹⁾ that oscillation does not take place so long as the gain · feedback product αβ is less than unity at the frequencies for which the phase shift is 180°. In a plot of αβ made on the complex plane, the requirement for stability is that the curve of αβ must not enclose the point 1, 0, with the sign of β considered opposite to that of α. Both gain α and feedback β are ratios of voltages. Therefore, both may be expressed in decibels and both are complex quantities at some frequencies. Proper care in application is required so that amplifiers with 180° or more phase shift do not oscillate at some frequency outside the pass band. If it is desired to correct for distortion or hum over a frequency range of 30 to 10,000 cycles, the amplifier should have low phase shift over a much wider range, say 10 to 30,000 cycles. In the frequency intervals of 10 to 30 cycles and 10,000 to 30,000 cycles, both the amplification and the feedback should taper off gradually to prevent oscillations.

Low phase-shift amplifiers benefit most from inverse feedback. Feedback in such amplifiers reduces size or improves performance, including phase shift. Transformer phase shift, therefore, is a vital property in feedback amplifiers and may take precedence over frequency response in some instances.

Fig. 131. Transformer-coupled amplifier low-frequency phase shift.

Phase shift at low and high frequencies is shown in Figs. 131 and 132 for transformer-coupled stages. At high frequencies, 180° phase shift is possible whereas at low frequencies but 90° is possible. In a resistance-coupled amplifier, only 90° phase shift occurs at either low or high frequencies. Partly for this reason, partly because less capacitance is incidental to resistors than to transformers and good response is maintained up to higher frequencies, it is in resistance-coupled amplifiers that inverse feedback is generally employed. But if the distortion of a final stage is to be reduced, transformer coupling is involved. It is preferable to derive the feedback voltage from the primary side of the output transformer. This is equivalent to tapping between R₁ and X_L in Fig. 132, where the phase shift is much less.

Fig. 132. Transformer-coupled amplifier high-frequency phase shift.

The transformer must still present a fairly high impedance load to the output tube throughout the marginal frequency intervals to permit gradual decrease of both amplification and feedback.

Current feedback is effected in the circuit of Fig. 133 by removing capacitor C. This introduces degeneration in the cathode resistor circuit, which accomplishes the same thing as the bucking action of voltage feedback. It is less affected by phase shift and consequently is used with transformer-coupled amplifiers.

Fig. 133. Cathode bias.

(1)	See "Regeneration Theory," by H. Nyquist, Bell System Tech. J., 11, 126 (January, 1932).