Limitations of Wave Filters

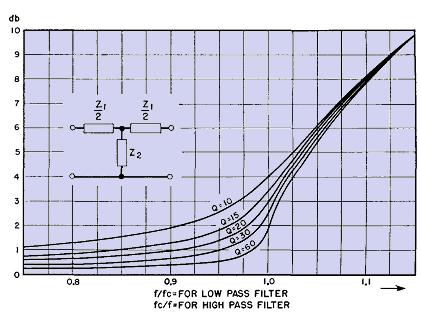
Several factors modify the performance of wave filters, shown in Fig. 136, especially in the cut-off region. One is the reflection due to mismatch of the characteristic impedance.⁽¹⁾ The load resistor is usually of constant value, whereas the image impedance changes to zero or infinity at cut-off for lossless filters. The resulting reflections cause rounding of the attenuation curve in the cut-off region instead of the sharp cut-off of Fig. 136.

Another cause of gradual slope at cut-off is the Q of the filter chokes, or ratio of reactance to resistance. Figure 137 gives the attenuation at cut-off in terms of Q for a section of the so-called constant-K filter (e.g., Fig. 135).

Fig. 137. Insertion loss near cut-off of a constant-K filter section.

Still another cause of the gradual slope of cut-off is the practice of inserting a resistor to simulate the source impedance in attenuation tests. In typical cases the source and terminating resistances are equal. The correct prediction of filter response near cut-off requires a good deal of care. It cannot be taken directly from the usual attenuation charts.

Phase shift is nearly linear with frequency up to approximately 50 per cent of cut-off frequency for constant-K filters in the transmission band. This fact is important in connection with networks used for the transmission of steep wave fronts, as in video amplifiers. It is proved in books on network theory⁽²⁾ that, when a non-sinusoidal voltage wave is applied to the input of a network, it appears at the output without distortion of its original shape if the phase shift of the network is proportional to frequency and if the amplitude response is flat for all frequencies. In no actual network are these conditions fulfilled completely, but the closer a network approximates them the smaller the distortion it causes in irregular wave forms. Linearity of phase shift is usually more essential to good wave form than flatness of response. For this reason, when a non-sinusoidal wave passes through a filter, distortion is minimized if the major frequency components of the wave all lie in the linear region of the phase shift curve. Considerable judgment must be exercised in the choice of cut-off frequencies. Higher-order harmonics are usually of smaller amplitude, and the natural tendency is to include too few of them in the pass band; then the output wave form is a poor reproduction of the input.

In band-pass filters, the effects just noticed are present, with the additional complication of band width. The filter designer must choose a band width of transmission such that high attenuation is afforded at unwanted frequencies and low attenuation at desired frequencies. This is often not a simple choice. For a given frequency separation from the mid-frequency, attenuation decreases as the filter band width is made wider. Impedance variation is much less with a wider band width. Therefore, choosing a narrow band width attenuates frequencies in the transmission band because of reflections.

(1)	See "An Analysis of Constant-if Low- and High-Pass Filters," by O. S. Meixell, RCA Rev., 5, 337 (January, 1941); also "Single-Section m-Derived Filters," by C. W. Miller, Wireless Engr., 21, 4 (January, 1944).
(2)	See Communication Networks, by E. A. Guillemin, John Wiley & Sons, New York, 1935, Vol. II, p. 474.