VIAS Encyclopedia: Error Surface

VIAS Encyclopedia provides a collection of tables and definitions commonly needed in science and engineering.

Home Mathematics Varia Error Surface	Index



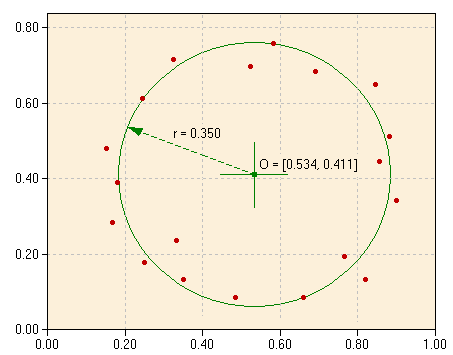
Error Surface An error surface is a (p+1)-dimensional surface representing the error terms of a model depending on p parameters. The coordinates of the error surface consist of the p parameters of the model function and the error term (this space is sometimes called the phase space). The error surface can be used to find the best fit of a model simply by searching the mimimum of the error surface. Example: Try to find the best fit of a circle to a set of data points The circle can be defined by the coordinates of the center O [x,y] and its radius r. Thus we have a model which depends on the three parameters (x, y, and r), forming a 3-dimensional space. Each possible circle can be specified by a point in this space. Next we calculate the sum of squared radial distances S_d between a particular circle [x,y,r] and the given data points u_i. The value of S_d will we different for each value of x, y, and r. It is evident that the best fit will be created by a circle which results in the smallest S_d. The values of S_d form a four-dimensional surface whose "height" will be a minimum at those parameters x, y, and r which describe the best fit circle. This surface is called the error surface. Error surfaces can be quite simple (as in the case of linear regression), or extremely complex (as e.g. for multimensional non-linear problems). In any case, one can use optimisation methods to find the minimum of the error surface (and thus solve the underlying problem).
Home Mathematics Varia Error Surface

Last Update: 2004-11-25