| The ebook FEEE - Fundamentals of Electrical Engineering and Electronics is based on material originally written by T.R. Kuphaldt and various co-authors. For more information please read the copyright pages. |

|

Home  Digital Digital  Digital-Analog Conversion Digital-Analog Conversion  Practical considerations of ADC circuits Practical considerations of ADC circuits  Resolution of ADC circuits Resolution of ADC circuits |
|






|
|
|
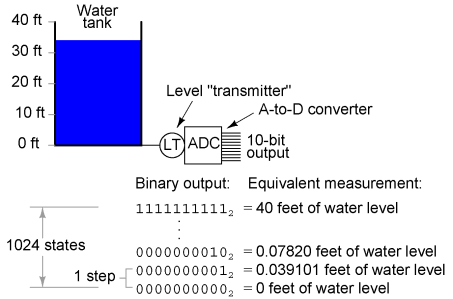
Resolution of ADC circuitsPerhaps the most important consideration of an ADC is its resolution. Resolution is the number of binary bits output by the converter. Because ADC circuits take in an analog signal, which is continuously variable, and resolve it into one of many discrete steps, it is important to know how many of these steps there are in total. An ADC can be seen of as some kind of device which applies a staircase function to the analog measurement, resulting in a discrete integer value. The more steps this function consists of the better is the resolution of the ADC. Of course, the number of bits required to encode all steps of the staircase function increases with the resolution of this function. 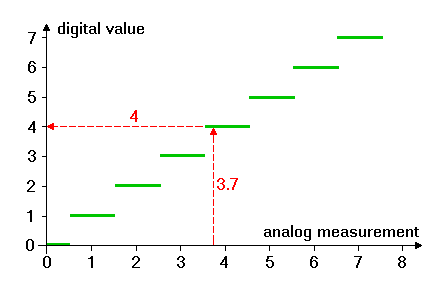
For example, an ADC with a 10-bit output can represent up to 1024 (210) unique conditions of signal measurement. Over the range of measurement from 0% to 100%, there will be exactly 1024 unique binary numbers output by the converter (from 0000000000 to 1111111111, inclusive). An 11-bit ADC will have twice as many states to its output (2048, or 211), representing twice as many unique conditions of signal measurement between 0% and 100%. Resolution is very important in data acquisition systems (circuits designed to interpret and record physical measurements in electronic form). Suppose we were measuring the height of water in a 40-foot tall storage tank using an instrument with a 10-bit ADC. 0 feet of water in the tank corresponds to 0% of measurement, while 40 feet of water in the tank corresponds to 100% of measurement. Because the ADC is fixed at 10 bits of binary data output, it will interpret any given tank level as one out of 1024 possible states. To determine how much physical water level will be represented in each step of the ADC, we need to divide the 40 feet of measurement span by the number of steps in the 0-to-1024 range of possibilities, which is 1023 (one less than 1024). Doing this, we obtain a figure of 0.039101 feet per step. This equates to 0.46921 inches per step, a little less than half an inch of water level represented for every binary count of the ADC.
This step value of 0.039101 feet (0.46921 inches) represents the smallest amount of tank level change detectable by the instrument. Admittedly, this is a small amount, less than 0.1% of the overall measurement span of 40 feet. However, for some applications it may not be fine enough. Suppose we needed this instrument to be able to indicate tank level changes down to one-tenth of an inch. In order to achieve this degree of resolution and still maintain a measurement span of 40 feet, we would need an instrument with more than ten ADC bits. To determine how many ADC bits are necessary, we need to first determine how many 1/10 inch steps there are in 40 feet. The answer to this is 40/(0.1/12), or 4800 1/10 inch steps in 40 feet. Thus, we need enough bits to provide at least 4800 discrete steps in a binary counting sequence. 10 bits gave us 1023 steps, and we knew this by calculating 2 to the power of 10 (210 = 1024) and then subtracting one. Following the same mathematical procedure, 211-1 = 2047, 212-1 = 4095, and 213-1 = 8191. 12 bits falls shy of the amount needed for 4800 steps, while 13 bits is more than enough. Therefore, we need an instrument with at least 13 bits of resolution.
|
|
Home  Digital Digital  Digital-Analog Conversion Digital-Analog Conversion  Practical considerations of ADC circuits Practical considerations of ADC circuits  Resolution of ADC circuits Resolution of ADC circuits |
|
Last Update: 2010-11-19