| The ebook FEEE - Fundamentals of Electrical Engineering and Electronics is based on material originally written by T.R. Kuphaldt and various co-authors. For more information please read the copyright pages. |

|

Home  DC DC  DC Metering Circuits DC Metering Circuits  Ammeter design Ammeter design |
||||






|
||||
|
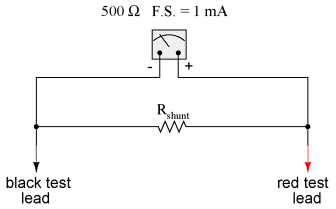
Ammeter designAmmeterA meter designed to measure electrical current is popularly called an "ammeter" because the unit of measurement is "amps."
Taking the same meter movement as the voltmeter example, we can see that it would make a very limited instrument by itself, full-scale deflection occurring at only 1 mA: As is the case with extending a meter movement's voltage-measuring ability, we would have to correspondingly re-label the movement's scale so that it read differently for an extended current range. For example, if we wanted to design an ammeter to have a full-scale range of 5 amps using the same meter movement as before (having an intrinsic full-scale range of only 1 mA), we would have to re-label the movement's scale to read 0 A on the far left and 5 A on the far right, rather than 0 mA to 1 mA as before. Whatever extended range provided by the parallel-connected resistors, we would have to represent graphically on the meter movement face.
Using 5 amps as an extended range for our sample movement, let's determine the amount of parallel resistance necessary to "shunt," or bypass, the majority of current so that only 1 mA will go through the movement with a total current of 5 A:
From our given values of movement current, movement resistance, and total circuit (measured) current, we can determine the voltage across the meter movement (Ohm's Law applied to the center column):
Knowing that the circuit formed by the movement and the shunt is of a parallel configuration, we know that the voltage across the movement, shunt, and test leads (total) must be the same:
We also know that the current through the shunt must be the difference between the total current (5 amps) and the current through the movement (1 mA), because branch currents add in a parallel configuration:
Then, using Ohm's Law (R=E/I) in the right column, we can determine the necessary shunt resistance:
Of course, we could have calculated the same value of just over 100 milli-ohms (100 mΩ) for the shunt by calculating total resistance (R=E/I; 0.5 volts/5 amps = 100 mΩ exactly), then working the parallel resistance formula backwards, but the arithmetic would have been more challenging:
In real life, the shunt resistor of an ammeter will usually be encased within the protective metal housing of the meter unit, hidden from sight. Note the construction of the ammeter in the following photograph:
This particular ammeter is an automotive unit manufactured by Stewart-Warner. Although the D'Arsonval meter movement itself probably has a full scale rating in the range of milliamps, the meter as a whole has a range of +/- 60 amps. The shunt resistor providing this high current range is enclosed within the metal housing of the meter. Note also with this particular meter that the needle centers at zero amps and can indicate either a "positive" current or a "negative" current. Connected to the battery charging circuit of an automobile, this meter is able to indicate a charging condition (electrons flowing from generator to battery) or a discharging condition (electrons flowing from battery to the rest of the car's loads). As is the case with multiple-range voltmeters, ammeters can be given more than one usable range by incorporating several shunt resistors switched with a multi-pole switch: 
Notice that the range resistors are connected through the switch so as to be in parallel with the meter movement, rather than in series as it was in the voltmeter design. The five-position switch makes contact with only one resistor at a time, of course. Each resistor is sized accordingly for a different full-scale range, based on the particular rating of the meter movement (1 mA, 500 Ω). With such a meter design, each resistor value is determined by the same technique, using a known total current, movement full-scale deflection rating, and movement resistance. For an ammeter with ranges of 100 mA, 1 A, 10 A, and 100 A, the shunt resistances would be as such:
Notice that these shunt resistor values are very low! 5.00005 mΩ is 5.00005 milli-ohms, or 0.00500005 ohms! To achieve these low resistances, ammeter shunt resistors often have to be custom-made from relatively large-diameter wire or solid pieces of metal. One thing to be aware of when sizing ammeter shunt resistors is the factor of power dissipation. Unlike the voltmeter, an ammeter's range resistors have to carry large amounts of current. If those shunt resistors are not sized accordingly, they may overheat and suffer damage, or at the very least lose accuracy due to overheating. For the example meter above, the power dissipations at full-scale indication are (the double-squiggly lines represent "approximately equal to" in mathematics):
An 1/8 watt resistor would work just fine for R4, a 1/2 watt resistor would suffice for R3 and a 5 watt for R2 (although resistors tend to maintain their long-term accuracy better if not operated near their rated power dissipation, so you might want to over-rate resistors R2 and R3), but precision 50 watt resistors are rare and expensive components indeed. A custom resistor made from metal stock or thick wire may have to be constructed for R1 to meet both the requirements of low resistance and high power rating. Sometimes, shunt resistors are used in conjunction with voltmeters of high input resistance to measure current. In these cases, the current through the voltmeter movement is small enough to be considered negligible, and the shunt resistance can be sized according to how many volts or millivolts of drop will be produced per amp of current:
If, for example, the shunt resistor in the above circuit were sized at precisely 1 Ω, there would be 1 volt dropped across it for every amp of current through it. The voltmeter indication could then be taken as a direct indication of current through the shunt. For measuring very small currents, higher values of shunt resistance could be used to generate more voltage drop per given unit of current, thus extending the usable range of the (volt)meter down into lower amounts of current. The use of voltmeters in conjunction with low-value shunt resistances for the measurement of current is something commonly seen in industrial applications. The use of a shunt resistor along with a voltmeter to measure current can be a useful trick for simplifying the task of frequent current measurements in a circuit. Normally, to measure current through a circuit with an ammeter, the circuit would have to be broken (interrupted) and the ammeter inserted between the separated wire ends, like this:
If we have a circuit where current needs to be measured often, or we would just like to make the process of current measurement more convenient, a shunt resistor could be placed between those points and left their permanently, current readings taken with a voltmeter as needed without interrupting continuity in the circuit:
Of course, care must be taken in sizing the shunt resistor low enough so that it doesn't adversely affect the circuit's normal operation, but this is generally not difficult to do. This technique might also be useful in computer circuit analysis, where we might want to have the computer display current through a circuit in terms of a voltage (with SPICE, this would allow us to avoid the idiosyncrasy of reading negative current values):
shunt resistor example circuit v1 1 0 rshunt 1 2 1 rload 2 0 15k .dc v1 12 12 1 .print dc v(1,2) .end v1 v(1,2) 1.200E+01 7.999E-04
We would interpret the voltage reading across the shunt resistor (between circuit nodes 1 and 2 in the SPICE simulation) directly as amps, with 7.999E-04 being 0.7999 mA, or 799.9 μA. Ideally, 12 volts applied directly across 15 kΩ would give us exactly 0.8 mA, but the resistance of the shunt lessens that current just a tiny bit (as it would in real life). However, such a tiny error is generally well within acceptable limits of accuracy for either a simulation or a real circuit, and so shunt resistors can be used in all but the most demanding applications for accurate current measurement.
|
||||
Home  DC DC  DC Metering Circuits DC Metering Circuits  Ammeter design Ammeter design |
||||
Last Update: 2010-12-01