Approximate Measurements

One of the first lessons which is learned by an experimenter making measurements on scientific methods is that the number obtained as a result is not a perfectly exact expression of the quantity measured, but represents it only within certain limits of error. If the distance between two towns be given as fifteen miles, we do not understand that the distance has been measured and found to be exactly fifteen miles, without any yards, feet, inches, or fractions of an inch, but that the distance is nearer to fifteen miles than it is to sixteen or fourteen. If we wished to state the distance more accurately we should have to begin by defining two points, one in each town - marks, for instance, on the doorsteps of the respective parish churches - between which the distance had been taken, and we should also have to specify the route taken, and so on. To determine the distance with the greatest possible accuracy would be to go through the laborious process of measuring a base line, a rough idea of which is given in §5. We might then, perhaps, obtain the distance to the nearest inch and still be uncertain whether there should not be a fraction of an inch more or less, and if so, what fraction it should be. If the number is expressed in the decimal notation, the increase in the accuracy of measurement is shown by filling up more decimal places. 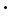Thus, if we set down the mechanical equivalent of heat at 4.210⁷ ergs, it is not because the figures in the decimal places beyond the 2 are all zero, but because we do not know what their values really are, or it may be, for the purpose for which we are using the value, it is immaterial what they are. It is known, as a matter of fact, that a more accurate value is 4.21410⁷, but at present no one has been able to determine what figure should be put in the decimal place after the 4.