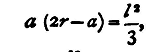| Practical Physics is a free textbook on basic laboratory physics. See the editorial for more information.... |

|

Home  Measurement of the More Simple Quantities Measurement of the More Simple Quantities  Length Length  The Spherometer The Spherometer |
||||||||
| See also: The Kathetometer, The Screw-Gauge | ||||||||






|
||||||||
The Spherometer
The spherometer consists of a platform with three feet, whose extremities form an equilateral triangle, and in the middle of the triangle is a fourth foot, which can be raised or lowered by means of a micrometer screw passing perpendicularly through the centre of the platform. The readings of the spherometer give the perpendicular distance between the extremity of this fourth foot and the plane of the other three.
The instrument is first placed on a perfectly plane surface - a piece of worked glass - and the middle foot screwed down until it touches the surface. As soon as this is the case, the instrument begins to turn round on the middle foot as a centre. The pressure of the hand on the screw should be very light, in order that the exact position of contact may be observed. The spherometer is then carefully removed from the glass, and the reading of the micrometer screw is taken. The figure (fig. 4) will help us to understand how this is done. ABC are the ends of the three fixed feet; D is the movable foot, which can be raised by turning the milled head at E. This carries round with it the graduated disc F G, and as the screw is turned the disc travels up the scale H K. The graduations of this scale are such that one complete revolution of the screw carries the disc from one graduation to the next Thus in the figure the point F on the screw-head is opposite to a division of the scale, and one complete turn would bring this point opposite the next division. In the instrument in the figure the divisions of the scale are half-millimetres, and the millimetres are marked 0, 1, 2. Thus only every second division is numbered.
But the rim of the disc F G is divided into fifty parts, and each of these subdivided into ten. Let us suppose that division 12 of the disc is opposite to the scale at F, and that the milled head is turned until division 36 comes opposite. Then the head has been turned through 24 (i.e. 36-12) larger divisions; but one whole turn or fifty divisions carry the point D through 1/2 mm. Thus a rotation through twenty-four divisions will carry it through 24/50 of 1/2 mm. or 0.24 mm. Hence the larger divisions on the disc F G correspond to tenths of a millimetre, and these are subdivided to hundredths by the small divisions. Thus we might have had opposite to the scale in the first instance 12.6 large divisions, and in the second 36.9. Then the point D would have moved through 0.243 mm. It will be noticed that in the figure division 0 is in the centre of the scale H K, which is numbered 1, 2, 3, &c., from that point in both directions up and down. The divisions numbered on the disc F G are the even ones1 - 2, 4, 6, &c. - and there are two numbers to each division. One of these numbers will give the parts of a turn of the screw when it is turned so as to lower the point D, the other when it is turned so as to raise D. Thus in the figure 12 and 38 are both opposite the scale, and in the second position, 36 and 14. We have supposed the head to be turned in such a way that the point D has been lowered through 0.24 mm. If the rotation had been in the opposite direction, D would have been raised through 0.26 mm. Let us for the present suppose that all our readings are above the zero of the scale. To take a reading we note the division of the scale next above which the disc stands, and then the division of the disc which comes opposite to the scale, taking care that we take the series of divisions of the disc which corresponds to a motion of the point D in the upward direction - the inner ring of numbers in the figure. Thus the figured reading is 1.380. If the instrument were in perfect order, the reading when it rested on a plane surface would be o-o. This is not generally the case, so we must observe the reading on the plane. This observation should be made four times, and the mean taken. Let the result be 0.460. Now take the instrument off the plane and draw the middle foot back some way. We will suppose we are going to measure the radius of a sphere from the convex side. Place the instrument on the sphere and turn, the screw E until D touches the sphere. The position of contact will be given as before, by noticing when the instrument begins to turn round D as a centre. Read the scale and screw-head as before; let the scale reading be: 2.5; and the disc 0.235. Then the reading is 2.735 mm. Take as before four readings. We require the distance through which the point D has been moved. This is clearly the difference between the two results, or 2.735 - 0.460; if we call this distance a we have a = 2.275 mm. It may of course happen that the reading of the instrument when on the plane is below the zero; in this case to find the distance a we must add the two readings. We must now find the distance in millimetres between the feet AB or AC. We can do this directly by means of a finely divided scale; or if greater accuracy is required, lay the instrument on a flat sheet of card or paper, and press it so as to mark three dots on the paper, then measure the distance between these dots by the aid of the beam-compass ( §2). Let us call this length l. Then we can show2 that, if r be the radius required,
The observation of l should be repeated four times. If we wish merely to test if a given surface is spherical, we must measure a for different positions of the apparatus on the surface, and compare the results; if the surface be spherical, the value of a will be the same for all positions. Experiments. (1) Test the sphericity of the given lens by observing the value of a for four different positions. (2) Determine the radius of the given sphere for two positions, and compare the results with that given by the calipers. Enter results thus:
|
||||||||
Home  Measurement of the More Simple Quantities Measurement of the More Simple Quantities  Length Length  The Spherometer The Spherometer |
||||||||
Last Update: 2011-03-27