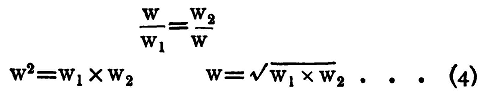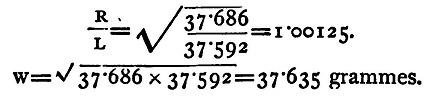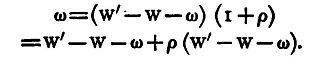| Practical Physics is a free textbook on basic laboratory physics. See the editorial for more information.... |

|

Home  Measurement of Mass and Specific Gravity Measurement of Mass and Specific Gravity  Testing the Adjustments of a Balance Testing the Adjustments of a Balance |
||||||||||||||||
| See also: Errors and Corrections | ||||||||||||||||






|
||||||||||||||||
Testing the Adjustments of a Balance
The method of weighing which we have described in the preceding section requires the balance to be in perfect adjustment But the only precaution for that purpose to which attention was called in the description was the levelling of the balance case. We previously mentioned, however (p. 84), that the centre of gravity of the beam could be made to be vertically under its axis of rotation by adjusting the metal flag attached to the beam, and we have, moreover, shown (pp. 88, 90) that the effect upon the weighings of the pointer not being properly placed, or of our not using the middle point of its scale as the zero, is inappreciable. We need consider, therefore, only the adjustment to equality of the weights of the scale pans and of the lengths of the arms. The former may, if necessary, be made equal by filing one of them until the necessary equality is attained, while the latter can be adjusted by means of the. screws which attach the end knife-edges to the beam.
The usual period of swing is about 15 seconds. Lord Rayleigh has, however, recently suggested (Brit Assoc. 1883) that the same accuracy of weighing with considerable saving of time may be secured by loading the pointer of the balance so that the time of swing is about 5 seconds, and using a magnifying glass to read the turning points of the pointer, and thus making up for the diminished sensitiveness by increased accuracy of reading. None of these adjustments should be carried out by any but practised observers with the balance, and not by them except after consultation with those who are responsible for the safe custody of the instrument. It is, however, very important for every observer to be able to tell whether or not the balance is in adjustment, and we therefore proceed to give practical directions for testing in such a manner as to measure the errors produced and enable us to allow for them. (1) To determine the Ratio of the Anns of a Balance, and to find the true Weight of a Body by means of a Balance with unequal Arms. Let ACB be the beam, and let R and L be the lengths of the arms CB and CA. Weigh a body, whose true weight is w, in the right-hand scale pan, and let the apparent weight be w1. Then weigh it in the left-hand pan, and let the apparent weight be w2. The weighing must be done as described in the previous section. Then we have
Provided that P Multiplying (1) by (2)
Dividing (1) by (2)
When w1 and w2 are nearly the same, we may put for sqrt(w1w2), 1/2(w1+w2), since the error depends on (sqrt(w1)-sqrt(w2))2, and this quantity is very small. (See p. 45).
Thus, if w1, w2 be the apparent weights of w in the two pans right and left respectively, the ratio of the arms is the square root of the ratio of w1 to w2. The true value of w is the square root of the product w1 Thus, if when weighed in the right pan, the apparent weight of a body is 37.686 grammes, and when weighed in the left, it is 37.592,
The true weight of a body may also be determined in a badly adjusted balance by the following method, known as the method of taring. Place the body in one scale pan and counterpoise it, reading the position of equilibrium of the pointer with as great accuracy as possible; then, leaving the same counterpoise, replace the body by standard weights, until the position of equilibrium of the pointer is the same as before. The mass which thus replaces the body is evidently that of the body, no matter what state the balance may be in. (This is called Borda's method.) (2) To Compare the Weights of the Scale Pans. Let a be the length of the arms supposed equal, s the weight of one pan, and s+ω that of the other. Weigh a body whose weight is Q first in the pan whose weight is s; let the apparent weight be w. Then interchange the scale pans and weigh Q again; let the weight be w'. Then
Divide each by a, and subtract; then ω = W'-W-ω, or ω = 1/2(W'-W). Thus, weigh the body in one pan; let its weight be w. Interchange the scale pans and weigh the body again in the other scale pan, but on the same side of the fulcrum; let the weight be w', then the difference in the weight of the scale pans is 1/2(w'-w). This will be true very approximately, even if the arms be not equal; for let one be R and the other L. Then we have
Now L/R is nearly unity; we may put it equal to 1+ρ, where ρ is very small.
But we suppose that ω, and therefore W'-W, is very small. Thus ω(W'-W-ω), being the product of two small quantities, may be neglected, and we get
Experiments. (1) Determine the ratio of the arms of the given balance. (2) Determine the difference between the weights of the scale pans. Enter as below: -
|
||||||||||||||||
Home  Measurement of Mass and Specific Gravity Measurement of Mass and Specific Gravity  Testing the Adjustments of a Balance Testing the Adjustments of a Balance |
||||||||||||||||
Last Update: 2011-03-27




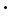 R = Q
R = Q