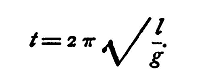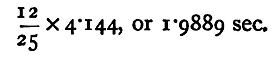The Pendulum

(1) To determine the Value of g by Observations with the Pendulum.

If t be the time of a complete oscillation of a simple pendulum whose length is l, and g the acceleration due to gravity, then it can be shown that

(See Maxwell, 'Matter and Motion,' chap, vii.) Thus,

We can therefore find the value of g by observing t, the time of a complete oscillation, and l the length of the pendulum.

A heavy sphere of metal suspended by a fine wire is, for our purposes, a sufficiently close representation of a simple pendulum. Corrections for the mass of the suspending wire, etc., can be introduced if greater accuracy be required.

To observe t, focus a telescope so that the wire of the pendulum coincides when at rest with the vertical cross-wire. A sheet of white paper placed behind the wire forms a suitable background. Set the pendulum swinging, and note by means of a chronometer or clock the times of four or five consecutive transits, in the same direction, of the pendulum across the wire of the telescope.

To obtain these with a pendulum beating at all rapidly, the best plan is to listen for the ticks of the clock, and count in time with them, keeping one eye at the telescope. Then note on a piece of paper the number of the tick at which each successive transit takes place.

Thus, suppose the clock beats half-seconds, we should obtain a series of numbers as below:

No. of transit	Hours	Minutes	Ticks
(1)	11	10	2
(2)	11	10	9
(3)	11	10	17
(4)	11	10	26
(5)	11	10	34
(6)	11	10	43

Thus, successive transits in the same direction occur at the following times:

No. of transit	Hours	Minutes	Ticks
(1)	11	10	1
(2)	11	10	4.5
(3)	11	10	8.5
(4)	11	10	13
(5)	11	10	17
(6)	11	10	21.5

Wait now for one or two minutes, and observe again Suppose we find there are transits at

No. of transit	Hours	Minutes	Ticks
(7)	11	14	9
(8)	11	14	13.5
(9)	11	14	17
(10)	11	14	22
(11)	11	14	26
(12)	11	14	40

Subtracting the time (1) from (7), (2) from (8), (3) from (9), etc., we get the times of a certain unknown but large number of oscillations.

The results are:

4 min	8 sec
4 min	9 sec
4 min	8.5 sec
4 min	9 sec
4 min	9 sec
4 min	8.5 sec

The mean is 4 min. 8.66 sec.

Thus, in 248.66 sec. there is a large whole number of complete oscillations.

Now, from our first series of observations we see that five complete oscillations occupy 20.5 sec. Thus, the time of an oscillation deduced from this series is ¹/₅ of 20.5 or 4.1 sec. From the second series the time of an oscillation is ¹/₅of 21, or 4.2 sec.

Thus, the time of a complete oscillation deduced from these two sets of observations is 4.15 sec.

If this were the true time of an oscillation, it would divide 248.66 sec. exactly. On doing the division, the quotient obtained is 59.92 sec.

This is very nearly 60, and since there has been a whole number of oscillations in the 248.66 sec. we infer that whole number must have been 60.

The time of an oscillation is therefore

t = 248.66 / 60 = 4.144 sec

The above is a specimen of the method generally employed to obtain an accurate measure of the time of an oscillation. It turns upon measuring roughly the time of oscillation and then determining the exact number of oscillations in a considerable interval by dividing the interval by the approximate measure of the time of oscillation, and selecting the nearest integer. One very important point in reference to this requires notice. Consider the instance quoted above. The rough value of the time of oscillation was determined by observing the time of five oscillations with a clock showing half-seconds. We must therefore consider the observation of the first and sixth transit as each liable to an error of half a second; that is, the time of the five oscillations is liable to an error of one second, and the calculated time of one is only to be regarded as accurate within 0.2 sec.

All we can be sure of, therefore, is that the time of an oscillation lies between 3.95 sec and 4.35 sec. Now the nearest integer to 248.66/3.95 is 63, and the nearest integer to 248.66/4.35 is 57; hence, without more observations than have been indicated above, we are not justified ia taking 60 as the proper integral number of oscillations during the interval. All we really know is that the number is one of those between 57 and 63.

In order that there may be no doubt about the proper integer to select, the possible error in the rough value of the time of oscillation, when multiplied by the integer found, must give a result less than half the time of an oscillation; thus in the instance quoted the inference drawn is a safe one, provided 4.15 sec represents the period of one oscillation to the thirtieth of a second. If this be the case the method given above will indicate the proper integer to select as representing the number of oscillations in 248 sec, and therefore give the time of an oscillation correct to about the 250th of a second.

There are two ways of securing the necessary accuracy in the observed time of an oscillation : (1) by making a series of thirty-one transit observations instead of 6, as indicated above; and (2) by repeating the process sketched, using intervals sufficiently small for us to be certain that we can select the right integer.

Thus, suppose six transit observations are made, the second series must be made after an interval not greater than 20 sec, a third after an interval of 60 sec. from the first, a fourth after an interval of 140 sec. From the original series a result will be obtained accurate to 0.2 sec.; with the first and second the accuracy can be carried to 0.1 sec., with the first and third to 0.05 sec.; and so proceeding in this way, we can with complete security carry the accuracy to any extent desired.

To determine l, we measure the length of the suspending wire by means of a tape, and add one half of the diameter of the bob as measured by the calipers. If the value of gravity is to be expressed in C. G. S. units (cm. per sec. per sec.), the length must be given in centimetres.

Thus the values of t and l have been found. Substituting these in the formula for g, its numerical value may be found. The value of π being 3.142, we may generally put π²=10 with sufficient accuracy.

(2) To compare the Times of Oscillation of two Pendulums. Method of Coincidences.

The method is only applicable in the case of two pendulums whose periods of oscillation are very nearly in some simple ratio which can be roughly identified.

The two pendulums are arranged one behind the other, and a screen is placed in front with a narrow vertical slit.

A telescope is arranged so as to view through the slit the nearer of the two wires. The second one is not visible, being covered by the first.

Let us suppose that the shorter pendulum vibrates rather more than twice as fast as the longer.

Start the two pendulums swinging; the two wires will appear to cross the slit at different moments. After a few swings they will cross in the same direction at the same moment.

We may notice that the shorter pendulum, besides executing two oscillations while the longer executes one, gradually gains on the latter, but after a time the two again cross simultaneously in the same direction. Let us suppose that this happens after 12 oscillations of the long pendulum; then there have been clearly 25 oscillations of the shorter in the same interval. Thus, the time of oscillation of the short pendulum is

If the longer pendulum had been gaining on the shorter, the latter would have lost one oscillation during the interval, and the ratio of the times of oscillation would have been 12 : 23.

Experiments.

(1) Determine by observations on a simple pendulum the value of g.
(2) Compare the times of oscillation of the two pendulums.

Enter results thus:

(1)

Approximate value of t (from 31 transits)	4.15 sec.
Corrected value from an interval of 4 min. 8.66 sec	4.144 sec
Length of suspending wire	421.2 cm.
Radius of bob	4.5 cm
Value of l	425.7 cm

(2) Ratio of times from rough observations: 2.1

Interval between coincidences twelve complete oscillations of the longer (the shorter pendulum gaining on the other).

Ratio of times: 2.083