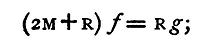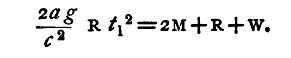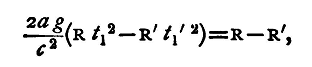Atwood's Machine

Two equal weights each of mass M are hung by a fine string over a pulley.

A third weight of mass R is allowed to ride on one of these two, thus causing it to descend. After it has fallen through a measured distance, R is removed by means of a ring, through which the weight carrying it can pass, while R cannot.

The time which it takes for the weights to fall through this measured distance is noted.

After R has been removed, the other weights continue moving, and the time they take to pass over another measured distance is observed.

Now, let us suppose that the height through which R falls before being removed is a centimetres and that the time it takes in falling is t seconds.

Let the space through which the weight continues to move downward be c centimetres, and the time taken t₁ seconds.

Then, if for the present we neglect the friction and momentum of the pulley which carries the weights, the mass being moved is 2M + R. The force producing motion is the weight of the mass R, and hence, if f be the acceleration

whence

Also, since R descends through a space a in t seconds, a = ft²/2; and if v be the velocity acquired by the weights at the time when R is removed, v = ft and v² = 2fa.

Thus, so long as the weights and rider R remain the same, we must have a proportional to the square of t.

The distance a is easily measured by means of a measuring tape.

Thus, let D (fig. 13) be the ring by which R is removed, and let A and B be the weights in their initial position.

Lower the tape from D to the ground, and note the division with which the top of A coincides. Then release the string and allow the weight to fall, noting the interval t. Next, by pulling the string, raise the weight B until its top comes level with the ring, and note the division of the tape opposite to which A stands.

The difference between these two readings gives the distance a.

Thus, in the figure, A stands at 12 ft. 8 in., when B comes to B' just passing the ring D, A has arrived at A', and the reading is 8 ft. 4 in. Thus

a=12 ft. 8 in. - 8ft. 4 in. = 4 ft. 4 in. = 132.08 cm.

We must now show how the time t may be conveniently measured.

This may be done by means of a metronome, a clockwork apparatus, which by adjusting a movable weight can be made to tick any required number of times - within certain limits - in a second. Adjust the weight so that the rate of ticking is as rapid as can conveniently be observed, and count the number of ticks in the time of fall. It will be an advantage if the metronome can be so adjusted that this shall be a whole number. Then determine the number of ticks per second, either by the graduations of the metronome or by taking it to a clock and counting the ticks in a known interval, and thus express the time of fall in seconds.

If a metronome is not obtainable, fairly accurate results may be obtained by allowing mercury to flow from a small nozzle through a hole in the bottom of a large flat dish, and catching in a weighed beaker, and then weighing the mercury which flows out while the weight is falling. The weight of mercury which flows out in a known interval of time is also observed, and by a comparison of the two weights the time required is determined.

The time t should be observed at least twice for the same fall a.

Now make the same observations with a different fall, a' suppose, and show that the law that the space traversed varies as the square of the time is true.⁽¹⁾

Now, let the weight B, after falling through the distance a, deposit R upon the ring D, and observe the time required by the weights A, B to pass over a further distance c; let it be t₁ seconds.

The weights move over the space c with uniform velocity v; thus t₁ the time of fall, is inversely proportional to v.

Now, v is the velocity acquired by falling through the distance a; thus v is proportional to the square root of a.

Thus, t₁ should be inversely proportional to the square root of a, or t₁² proportional to 1/a.

Thus, at² should be constant, and equal to c²/2f. Observe the value of t₁ for various values of a, and show that at₁² is constant.

From the last observations we can calculate the value of g, the acceleration due to gravity.

For if f be the acceleration produced by the weight of the mass R,

M and R are the number of grammes in the weights used.

We have neglected the effect of the momentum produced in the pulley and of friction.

We can allow for the former in the following manner:

It can be shown theoretically that its effect is practically to increase the mass moved without altering the force tending to produce motion. Thus we should include in the mass moved a quantity w, which we can calculate by theory, or better determine by experiment.

Thus, if f as before be the acceleration,

Repeat the observations, using the same value of c and a, but altering the rider to R'; t₁ will be changed to t₁', and the acceleration will be f' where

But

Hence

and

To eliminate the effect of friction we may determine experimentally the least mass which we must attach to the weight B in order just to start the apparatus. Let this be F grammes. Then, if we assume the friction effect to be constant throughout the experiment, the part of R which is effective in producing acceleration is R-F; we must therefore substitute R-F for R throughout.

It is probably not true that the frictional effect is the same throughout; the apparatus is, however, so constructed that it is very small, and a variation from uniformity is unimportant.

The string by which the weights are hung is generally thin; be careful therefore lest it break.

Experiments.

(1) show from three observations that the space through which a mass falls in a given time is proportional to the square of the time.
(2) show with the above notation from three observations that at? is a constant.
(3) Determine the .value of g, using two or three different masses as riders.
(4) Obtain from your results with two of these riders a value for g corrected for the inertia of the pulley.
(5) Correct your result further for the friction of the pulley.

Enter results as below:

Exp. 1.

Value of a	Value of t	Ratio a/t2
400 cm	7.5 sec	7.1
300 cm	6.5 sec	7.1
200 cm	5.4 sec	6.9

Exp. 2.

Value of a	Value of t1	Ratio a*t12
400 cm	4.3 sec	739
300 cm	4.9 sec	720
200 cm	6.1 sec	744

Exp. 3

a = 400 cm.	c = 450 cm
M = 300 gm
R = 10 gm	t1 = 4.3 sec
R' = 8 gm	t1' = 4.5 sec
R" = 6 gm	t1" = 5.2 sec

Values of g respectively: 945, 942, and 946

(1)	If the apparatus can be arranged so that the distance a can be varied, more accurate results may be obtained by determining the value of a, for which the time t is an exact multiple of the period of the clock or metronome.