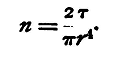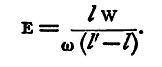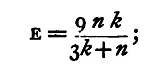Summary of the General Theory of Elasticity

The elastic properties of an isotropic homogeneous elastic body depend on two qualities of the body - viz. its compressibility and its rigidity. The compressibility determines the alteration in volume due to the action of external forces, the rigidity the alteration in form.

Compressibility and Elasticity of Volume.

Suppose we have a body whose volume is V, and that it is under a hydrostatic pressure P; let the pressure be changed to P+p, and the volume in consequence to V-v. Then v/V is the change in unit volume due to the increment of the pressure p, and v/(V/p) is the change per unit volume due to unit increment of pressure.

This is called the compressibility of the body, which may be defined as the ratio of the cubical compression per unit volume to the pressure producing it. The reciprocal of the compressibility - viz. the value of vp/V - is the elasticity of volume. We shall denote it by k.

Rigidity.

Any alteration of form or of volume in a body is accompanied by stresses and strains throughout the body.

A stress which produces change of form only, without alteration of volume, is called a shearing stress.

Imagine one plane in the body to be kept fixed while all parallel planes are moved in the same direction parallel to themselves through spaces which are proportional to their distances from the fixed plane; the body is said to undergo a simple shear.

Suppose further that this simple shear is produced by the action of a force on a plane parallel to the fixed plane, and uniformly distributed over it; then the ratio of the force per unit of area to the shear produced is defined to be the rigidity of the body.

Let T be the measure of the force acting on each unit of area of the plane, and suppose a plane at a distance a from the fixed plane is moved through a distance c; then c/a is defined as the measure of the shear, and the rigidity of the body is Ta/c.

Let us call this n. It may be shown mathematically that, if a circular cylinder of radius r and length l be held with one end fixed, the couple required to turn the other end through an angle θ is nπr⁴θ/2l.

Modulus of Torsion.

The couple required to twist one end of unit length of a wire through unit angle, the other end of the wire being kept fixed, is called the modulus of torsion of the wire.

Hence if τ be the modulus of torsion, the couple required to twist one end of a length l through an angle θ, the other end being kept fixed, is τθ/l.

Relation between Modulus of Torsion and Rigidity.

We have given above two expressions for the couple required to twist one end of a length l of a wire of circular section through an angle θ, the other end being kept fixed; equating these two expressions we get for a wire of radius r,

Youngs Modulus.

If an elastic string or wire of length l be stretched by a weight w until its length is l', it is found that (l'-l)/lw is constant for that wire, provided that the wire is not strained beyond the limits of perfect elasticity; that is, the weight w must be such that, when it is removed, the wire will recover its original length.

If the cross section of the wire be of unit area, the ratio of the stretching force to the extension per unit length is called Young's Modulus, for the material of which the wire is composed, so that if the cross section of the wire be ω sq. cm. and we denote Young's Modulus by E, we have

Relation between Youngs Modulus and the Coefficients of Rigidity and Volume Elasticity.

We can show from the theory of elasticity (see Thomson, Ency. Brit. Art. 'Elasticity'), that if E be Young's Modulus,

and hence

Thus, knowing E and n, we can find k.