The Mercury Barometer

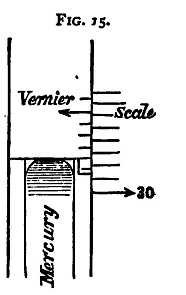
Barometers are of various forms; the practical details given here are intended with reference to the Fortin Standard Barometer, in which the actual height of the column of mercury, from the surface of the mercury in the cistern, is measured directly by means of a scale and vernier placed alongside the tube. The scale is only graduated between twenty-seven and thirty-two inches, as the barometric height at any ordinary observatory or laboratory is never outside these limits.

To set and read the Barometer.

The barometer must first be made to hang freely, by loosening the three screws at the bottom of the frame, in order that the scale may be vertical.

The mercury in the cistern must be brought to the same level as the zero point of the scale. This zero point is indicated by a small ivory point; and the extremity of this point must first be made to coincide with the surface of the mercury.

This is attained by adjusting the bottom of the cistern by means of a screw which projects from the bottom of the barometer; raising this screw raises the mercury surface. On looking at the surface a reflexion of the pointer is seen. Raise the surface until the end of the pointer and its reflected image appear just to touch. Then the mercury surface and the zero of the scale are at the same level.

The upper surface of the mercury is somewhat convex. In taking a reading, the zero of the vernier must be brought to the same level as the top point of this upper surface.

Behind the barometer tube is placed a sheet of white paper, and by raising the vernier this can be seen, through the tube, between it and the upper surface of the mercury.

Lower the vernier until,⁽¹⁾ looking horizontally, it is just impossible to see the white paper between it and the top of the meniscus; then, the zero of the vernier coincides with the top of the mercury column. To be able to make sure that the eye looks horizontally the vernier is provided with a brass piece on the opposite side of the tube, the lower edge of which is on the same level as the lower edge of the vernier when the scale is vertical. By keeping the eye always in a line with these two edges we know that the line of sight is horizontal, and thus avoid error of parallax. Of course a glimpse of white may be obtained at the sides, owing to the curvature of the meniscus, as in the figure.

The scale is in inches, and is divided to twentieths. Twenty-five divisions of the vernier are equal to twenty-four of the scale; the instrument therefore reads to 500ths of an inch.

To read it rapidly; divide the reading of fractions of the inch on the scale by 2; the result is in tenths of an inch; multiply the vernier reading by 2; the result is in thousandths of an inch.

Thus suppose that the scale reading is 30 inches and three divisions. This is 30.15. The vernier reading is 13, and this is 0.026 inch; the reading then is 30.176 inches.

This reading may be reduced to millimetres by the following table:

mm.	Inches		mm.	Inches
710	27.9532		760	29.9217
720	28.3469		770	30.3I55
730	28.7406		780	30.7091
740	29.1343		790	31.1029
750	29.5280		800	31.4966

Thus 30.176 inches=766.45 mm.

Correction of the Observed Height for Temperature

The height thus obtained requires several corrections.

(1) Mercury expands with a rise of temperature, and we must therefore reduce our observation to some standard temperature, in order to express the pressure in comparable measure. The temperature chosen is 0°C, and the coefficient of expansion of mercury is 0.000181 per °C. Thus, if l be the observed height and t the temperature, the height of the equivalent column at 0°C. is l(1-0.000181t). In applying this correction, it is very often sufficient to use the mean value, 760 mm. for l, in the small term 0.000181tl.

Now 760 x 0.000181 = 0.138. Then we can get the corrected height with sufficient approximation by subtracting from the observed height 0.138t. Thus if the observed height be 766.45 mm. and the temperature 15°, the true height, so far as this correction only is concerned, is

(2) The same rise of temperature has caused the brass scale to expand, so that the apparent height of the column is on that account too short. To obtain the true height we must add to the observed height l, the quantity lβt, β being the coefficient of linear expansion of brass.

Now β = 0.000019. The complete correction then due to both causes will be - (0.000181 - 0.000019)tl and the true height is l - (0.000181 - 0.000019)tl or l-0.000162tl.

If in the small term, 0.000162tl, we take the mean value, 760 mm., for l, the true height is b, where b=l-0.123t. Thus in our case t=15°C,

(3) Owing to the capillary action between the glass of the tube and the mercury, the level of the mercury is depressed by a quantity which is roughly inversely proportional to the diameter of the tube. The depression is not practically of an appreciable amount unless the tube has a diameter less than a centimetre.

In the instrument in the Cavendish Laboratory the tube is 5.58 mm. in radius, and in consequence the top of the meniscus is depressed by about 0.02 mm.; we must therefore add this to the observed height, and we find that the corrected value of the height is 767.62 mm.

(4) Again, there is vapour of mercury in the tube, which produces a pressure on the upper surface of the column. It is found that at temperature t this may be practically taken to be equivalent to 0.002t mm. of mercury. Thus, if the temperature be 15°, we must on this account add to the observed height 0.03 mm., and we obtain as our corrected height 764.65 mm. This is the true height of the column of mercury at standard temperature, which gives a pressure equivalent to the pressure of the atmosphere at the place and time in question.

(5) Now the weight of this column is balanced against the pressure of the air. The weight of the column will depend on its position relatively to the earth. We must therefore determine the height of the column which at some standard position will weigh as much as our column. We take for that standard position sea-level in latitude 45°.

Let g₀ be the value of the acceleration due to gravity at this position, b₀ the height of a column weighing the same as our column b; g the acceleration due to gravity at the point of observation.

Then, since the weights of these two columns are the same, we have b₀g₀=bg and therefore b₀=bg/g₀.

Now it is known from the theory of the figure of the earth that if h is the height above the sea-level in metres and φ the latitude of the place of observation,

Hence

Experiment. - Read the height of the standard barometer, and correct to sea-level at 45° lat.

(1)	See Frontispiece, fig. 2.