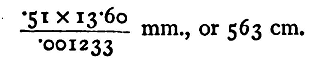The Aneroid Barometer

In the aneroid barometer at the Cavendish Laboratory each inch of the scale is divided into fiftieths, and there is a vernier,⁽¹⁾ twenty half-divisions of which coincide "with twenty-one of the scale; the vernier reads, therefore, by estimation to thousandths of an inch. On the vernier each division must be counted as two, only the even divisions being marked.

The aneroid is set by comparison with a corrected mercury-barometer, to give the true pressure at the time of the observation. If properly compensated for temperature, it would continue to give the true barometric height at any other station, even if the temperature changes.

To read the aneroid, set the zero of the vernier exactly opposite the end of the pointer, and read the inches and fiftieths on the scale up to the vernier zero.

Multiply the fractional divisions by 2; the result is in hundredths of an inch. Read the vernier, and again multiply by 2; the result is in thousandths of an inch.

(The numbers marked on the scale give tenths of an inch; those on the vernier thousandths.)

Thus the scale reading is between 30 and 31, the pointer standing between divisions 12 and 13. The scale reading, therefore, is 30.24. When the zero of the vernier is opposite the pointer there is a coincidence at division 8 of the vernier; the vernier reading is, therefore, 0.016, and the exact height is 30.256.

To measure the height between two stations with the aneroid, take the reading at the two stations and subtract The difference gives the pressure in inches of mercury of the column of air between the two.

Thus suppose that at a lower station the reading of the aneroid is 30.276, and the difference in pressure is that due to 0.020 inch of mercury; this is equivalent to 0.51 mm.

The specific gravity of mercury is 13.60; thus 0.51 mm. mercury is equivalent to 0.51 x 13.60 mm. of water at 4°C.

To find the true height of the column of air which is equivalent in pressure to this, we must divide by the specific gravity of air at the temperature and pressure of observation. This may be determined when the pressure and temperature have been observed, by calculation from the data given in No. 36 of Lupton's 'Tables.'

If the difference of height is not great the pressure of the air between the two stations may, for this purpose, be taken to be the mean of the aneroid readings at the two stations, properly corrected by reference to the mercury standard. For the temperature, if there is any considerable difference between the thermometer readings at the two stations, some judgment must be used in order to get a mean result which shall fairly represent the average temperature of the air between the two. When these observations have been made, we are in a position to calculate the specific gravity of dry air under the given conditions. Since the atmosphere always contains more or less moisture, a correction must be applied. Since the specific gravity of aqueous vapour referred to air at the same temperature and pressure is ⁵/₈, the correction may be made by calculating what would be the specific gravity of the dry air if its pressure were diminished by an amount equivalent to three-eighths of the pressure of the water vapour it contains, as determined by observation of the dew-point or other hygrometric method. This correction is often so small as to produce no appreciable effect within the limits of accuracy of the pressure readings.

Thus if the mean of the pressure observations be 768 mm., and the estimated mean temperature 15°C, the specific gravity of dry air would be 0.001239, and if the observed pressure of aqueous vapour be 10 mm., the corrected specific gravity would be

Hence the height of the column of air between the two stations is

For a method of extending the application of barometric observations to the measurement of comparatively greater heights we may refer the reader to Maxwell's 'Heat', Chap. XIV.

Experiment - Read the aneroid and determine from your observation of the standard the correction to be applied to the aneroid to give the true reading.

Measure the height of the laboratory from the basement to the tower.

(1)	See Frontispiece, fig. 4.