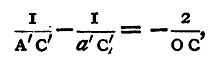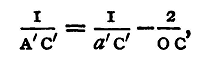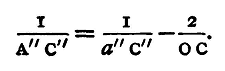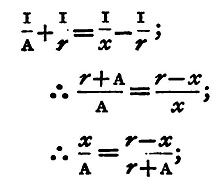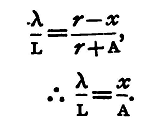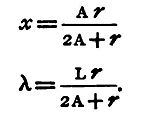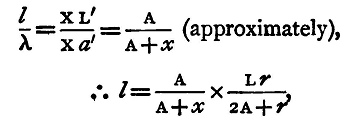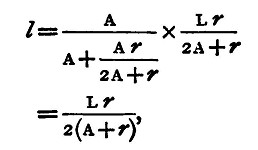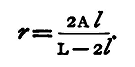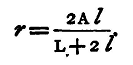Measurement of the Radius of Curvature of a Reflecting Surface by Reflexion

The method of §49 is applicable only when the reflecting surface is concave, so that the reflected image is real. The following method will do for either a concave or convex surface.

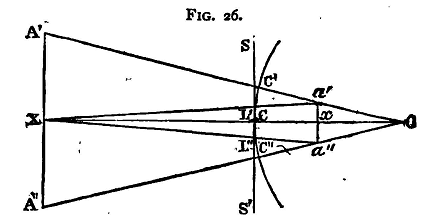
Let O, fig. 26, be the centre of the reflecting surface, OCX the axis.

Suppose two objects A', A" (which may be two lamps or bars of a window) placed at equal distances on each side of OCX, and at the distance OX from O.

Images of these two points will be formed by reflexion at points a', a" on the axes OA', OA", such that (calling the points where the axes OA, OA' cut the spherical surface C', C")

or

and

Now, the points being very distant, and therefore C'A' very nearly equal to CX, we may assume that the straight line a'a" cuts the axis OCX at a point x where

and for the size of the image, we have

Hence, if CX = A, OC = r, A'A" = L, Cx=x, and a'a" = λ we get from (1)

Hence

and

From these two equations

Place a small, finely divided scale SS' immediately in front of the reflecting surface (but not so as to prevent all the light falling upon it) i.e. place it horizontally to cover nearly half the reflecting surface, and observe the images a', a" and the scale SS' by means of a telescope placed so that its object-glass shall be as nearly as possible in the middle of the line joining AA'; we may with sufficient accuracy suppose the centre of the object-glass to be at the point X. Join Xa, Xa' and let the lines Xa, Xa" cut the scale SS' in L' and L", and let l denote the length L'L" of the scale intercepted by them.

Then we get

or

or

The formula proved above refers to a convex surface; if the surface be concave we can find similarly the equation

To make use of this method to find the radius of curvature of a surface, place the surface opposite to, but at some distance from, a window. Then place horizontally a straight bar of wood, about half a metre in length between the surface and the window, fixing it approximately parallel to the surface, and at such a height that its reflexion in the surface is visible to an eye placed just below the bar, and appears to cross the middle part of the surface. Fix a telescope under the centre of the bar, with its object-glass in the same vertical plane as the bar, and focus it so as to see the image reflected in the surface.

It is best that the whole of the bar should be seen reflected in the surface. If this cannot be secured, two well-defined marks, the reflected images of which can be clearly seen, should be made on the bar. These may be obtained by fixing two strong pins into the upper edge, or by laying on it two blocks of wood with clearly defined edges.

In any case the reflected image should appear in the telescope as a well-marked dark object against the bright background of the reflexion of the window. If it be more convenient to work in a dark room, arrangements must be made to illuminate the bar brightly, so that its reflexion may appear light against a dark background.

Now place against the reflecting surface a finely graduated scale - one divided to half-millimetres or fiftieths of an inch will do - arranging it so that one edge of the image of the bar is seen against the divided edge of the scale. If the curvature of the surface be considerable, and the magnifying power of the telescope not too great, the scale will be fairly in focus at the same time as the image of the bar. At any rate, it will be possible to read the graduations of the scale which the image of the bar appears to cover. This gives us the length l of the above formula. Measure the length of the bar or the distance between the two marks - this we call L; and measure with a tape the distance between the reflecting surface and the centre of the object-glass of the telescope - this gives A.

Then the formula gives us r.

In some cases it may be possible to see more than one reflected image of the bar; e.g. if a reflecting surface be one surface of a lens, we may have a reflexion from the back surface as well as from the front. A little consideration enables us to choose the right image. Thus, if the first surface is convex, the reflected image will be erect and will, therefore, appear inverted if we are using an astronomical telescope.

Experiment - Determine the radius of the given surface, checking the result by the use of the spherometer.

Enter results thus: -