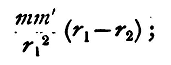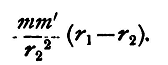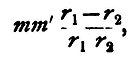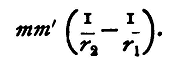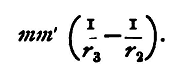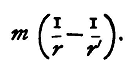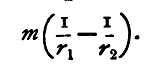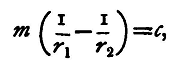| Practical Physics is a free textbook on basic laboratory physics. See the editorial for more information.... |

|

Home  Magnetism Magnetism  Magnetic Potential Due to a Single Pole Magnetic Potential Due to a Single Pole |
|






|
|
Magnetic Potential Due to a Single Pole
The force between two magnetic poles of strengths m and m' at a distance r1 centimetres apart is, we have seen, a repulsion of mm'/r2 dynes. Let us suppose the pole m' moved towards m through a small distance. Let A (fig. 42) be the position of m, P1, P2 the two positions of m'. Then AP2P1 is a straight line, and AP1 = r1. Let AP2 = r2, P1P2 = r1-r2.
Then, if, during the motion, from P1 to P2, the force remained constant and of the same value as at P1, the work done would be
while if, during the motion, the force had retained the value which it has at P2, the work would have been
Thus the work actually done lies between these two values. But since these fractions are both very small, we may neglect the difference between r1 and r2 in the denominators. Thus the denominator of each may be written r1r2 instead of r12 and r22 respectively. The two expressions become the same, and hence the work done is
or
Similarly the work done in going from P2 to a third point, P3, is
And hence we see, by adding the respective elements together, that the work done in going from a distance r' to a distance r is
Hence the work done in bringing the pole m' from infinity to a distance r from the pole m is mm'/r. But the potential due to m at a distance r, being the work done in bringing up a unit pole from beyond the influence of the pole m, will be found by dividing this by m'; it is therefore equal to m/r. Again, it follows from the principle of conservation of energy that the work done in moving a unit pole from any one point to any other is independent of the path, and hence the work done in moving the unit pole from any point whatever at a distance r' to any point at a distance r from the pole m is
For a single pole of strength m, the equipotential surfaces are clearly a series of concentric spheres, with m as centre; the lines of force are radii of these spheres.
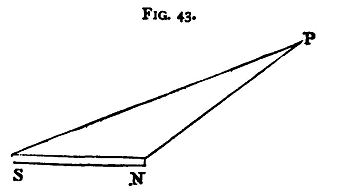
If we have a solenoidal magnet of strength m, and r1, r2 be the distances of any point, P (fig. 43), from the positive and negative poles N and S of the magnet, then the potential at P due to the north pole is m/r1, and that due to the south pole is -m\r2; hence the potential at P due to the magnet is
The equipotential surfaces are given by the equation
where c is a constant quantity, and the lines of force are at right angles to these surfaces. To find the resultant magnetic force at P we have to compound a repulsion of m\r12 along NP with an attraction of m\r22 along PS, using the ordinary laws for the composition of forces. Let us now consider the case in which the lines of force in the space in question are a series of parallel straight lines uniformly distributed throughout the space. The intensity of the field will be the same throughout; such a distribution constitutes a uniform magnetic field. The earth is magnetic, and the field of force which it produces is practically uniform in the neighbourhood of any point provided that there be no large masses of iron near, and the lines of force are inclined to the horizon in these latitudes at an angle of about 67°.
|
|
Home  Magnetism Magnetism  Magnetic Potential Due to a Single Pole Magnetic Potential Due to a Single Pole |
|
Last Update: 2011-03-16