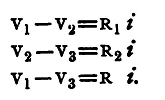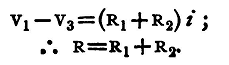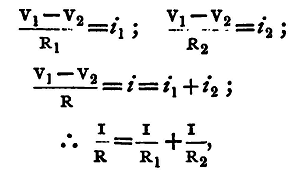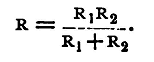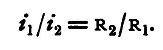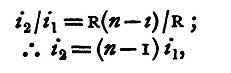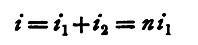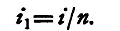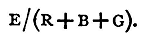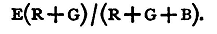Resistance of Conductors in Series

If AB, BC be two conductors of resistances R₁ and R₂, the resistance between A and C is R₁+R₂. For let the potentials at A, B, C be V₁, V₂, V₃ respectively, and suppose that owing to the difference of potential a current i is flowing through the conductors. This current is the same in the two conductors (see p. 386), and if R be the resistance between A and C, we have from Ohm's law

But by adding the first two equations we have

By similar reasoning it may be shown that the resultant resistance of any number of conductors placed end to end is equal to the sum of the resistances of the several conductors. Conductors connected in this manner are said to be in series.

Again, let there be two conductors of resistances R1, R2, joining the same two points A and B, and let R be the equivalent resistance of the two, that is, the resistance of a conductor, which, with the same E.M.F. would allow the passage of a current of electricity equal to the sum of those which actually flow in the two conductors. Hence, if V₁, V₂ be the potentials at A and B, we have

and

Also

Conductors joined up in the above manner are said to be connected in multiple arc; thus, remembering that the reciprocal of the resistance is called the conductivity, we may show by reasoning precisely similar to that given above that the conductivity of a system of any number of conductors in multiple arc is the sum of the conductivities of the several conductors.

Let BAC be a circuit including a battery B, and suppose that we wish to send between the two points, A and C, only 1/nth part of the current produced by the battery. Let R be the resistance between A and C. Connect these two points by a second conductor of resistance, R/(n-1).

Let i₁ be the current in the original conductor between A and C, i₂ the current in the new conductor, i the current in the rest of the circuit. Then we have

and

So that

The second conductor, connected in this manner with the two points, is called a shunt, and the original circuit is said to be shunted.

Shunts are most often used in connection with galvanometers. Thus we might require to measure a current by the use of a tangent galvanometer, and, on attempting to make the measurement, might find that the galvanometer was too sensitive, so that the deflexion produced by the current was too large for measurement By connecting the electrodes of the galvanometer with a shunt of suitable resistance we may arrange to have any desired fraction of the current sent through the galvanometer.

This fraction can be measured by the galvanometer, and the whole current is obtained from a knowledge of the resistances of the shunt and galvanometer. A galvanometer is often fitted with a set of shunts, having resistances 1/9, 1/99, and 1/999 of its own resistance, thus enabling 0.1, 0.01, or 0.001 of the whole current to be transmitted through it.

In applying Ohm's law to a circuit in which there is a battery of electromotive force E, it must be remembered that the battery itself has resistance, and this must be included in the resistance of the circuit. Thus, if we have a circuit including a resistance R, a battery of E.M.F. E and resistance B, and a galvanometer of resistance G, the total resistance in the circuit is R+B+G, and the current is

The normal E.M.F. of the battery is taken to be the difference of potential between its poles when they are insulated from each other. If they be connected together, the difference of potential between them will depend on the resistance of the conductor joining them. In the case in point this is R+G; and since the difference of potential is found by multiplying together the current and the resistance, it will in that case be