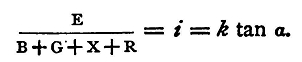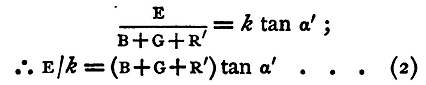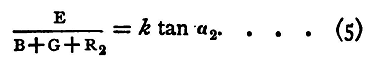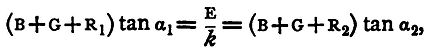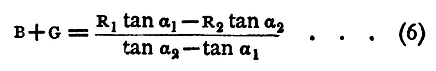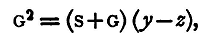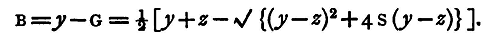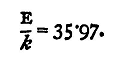Comparison of Electrical Resistances

Ohm's law forms the basis of the various methods employed to compare the electrical resistance of a conductor with that of a standard coil.

In the simplest arrangement of apparatus for making the measurements the connections are made in the following manner (fig. 62): One pole of a battery B of constant E.M.F. is connected to one end A of the conductor whose resistance is required; the other end C of this conductor is in connection with a resistance box MN. N is in connection with a key or, better, a commutator K, from which the circuit is completed through a galvanometer G to the other pole of the battery.

Let X be the resistance to be measured, B the battery resistance, G that of the galvanometer, and suppose a resistance R is in circuit in the box.

Make contact with the commutator. A current passes through the galvanometer. Observe the deflexion when the needle has become steady. Reverse the commutator; the galvanometer needle is deflected in the opposite direction, and if the adjustments were perfect, the two deflexions would be the same. They should not differ by more than 0.5°.

Adjust R, the resistance in the box, if it be possible, until the deflexion observed is about 45°. Of course it may be impossible to do this with the means at hand. If when R is zero the deflexion observed be small, the electromotive force of the battery will require to be increased; we must use more cells in series. If, on the other hand, with as great a resistance in the box as is possible, the deflexion be too large, then either the galvanometer must be shunted or the E.M.F. of the battery reduced by reducing-the number of cells, or by connecting its poles through a shunt. In any case the deflexion should be between 30° and 60°.

Let E be the E.M.F. and k the reduction factor of the galvanometer, which, we shall suppose, is a tangent instrument. Then, if i be the current, and α the mean of the two deflexions in opposite directions, we have

Hence

and if B, G, E, and k be known, R and a being observed, this equation will give us X.

If E and k be not known, while B and G are, we proceed thus. Take the unknown resistance X out of the circuit, connecting one pole of the battery with the electrode M of the resistance box. Take a resistance R' out of the box and observe the deflexion, which, as before, should lie between 30° and 60°, reversing the current and reading both ends of the needle; let the mean deflexion be of. Then we have, as before, if the battery have a constant E.M.F.,

so that the original equation (1) becomes

and from this X can be found.

But in general B and G will not be known. We can easily find the sum B+G as follows:

Make two sets of observations exactly in the same manner as the last were made, with two different resistances R₁, R₂ out of the box, and let the deflexions be α₁ and α₂; α₁ may be just over 30°, aa just under 60°.

[There should be a large difference between α₁ and α₂, for we have to divide, in order to find the result, by tanα₂ - tanα₁ and, if this be small, a large error may be produced.]

Then, assuming as before that the E.M.F. of the battery does not alter, we have

and

Hence

and

Having thus found B+G, we may use either of the equations (4) or (5) in combination with (1) to give us X.

If we wish to find B and G separately we may proceed as follows:

Shunt the galvanometer with a shunt of resistance S; then the resistance between the poles of the galvanometer is equivalent to GS/(S+G). Make two more observations like those from which equations (4) and (5) are deduced, we thus find a value for B+GS/(S+G).

Suppose we find

having already obtained

when y is written for the right-hand side of equation (6). Hence

thus

or

Thus, G having been found, B is given from the equation

The methods here given for measuring resistance, involving, as they do, the assumption that the E M.F. of the battery remains the same throughout, cannot be considered as completely satisfactory. Others will be given in §§77-79, which are free from the objections which may be urged against these. Various modifications of the above methods have been suggested for measuring more accurately the resistance of a battery or galvanometer. For an account of these the reader is referred to Kempe's 'Handbook of Electrical Testing,' chapters v. and vi. In practice much is gained by a little judgment in the choice of the resistances taken from the box. Thus, in finding B+G as above it might happen that when R₂ is 19, α₂ is 59°30', and when R₂ is 20, α₂ is 58°45'. Now the tangent of either of these angles can be looked out equally easily in the tables, but the multiplication involved in finding R₂tanα₂ is much more easily done if R₂ be 20 than if it be 19.

Experiment. - Determine the resistance of the given coil X. Enter results thus : -

Observations to find B + G.

Observations to find X.

N.B. - If a large number of resistances have to be determined by the use of the same galvanometer, it will be best to calculate the value of B + G, and the ratio of the E.M.F. to the reduction factor once for all, checking the results occasionally during the other observations. These are both given by the observations just made, for we have found B + G, and we have

With the numbers in the above example,

and we find

So that, if we find, with an unknown resistance X in circuit and a resistance R out of the box, that the deflexion is a, we obtain