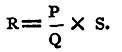Measurement of a Galvanometer Resistance - Thomson's Method

It has been shown that if, in the Wheatstone's bridge arrangement, two of the conductors, as AB, CD (fig. 66, p. 442), are conjugate, then the current through the one due to an E.M.F. in the other is zero. It follows from this that the current through the other conductors is independent of the resistance in CD, and is the same whether CD be connected by a conductor or be insulated; for the condition that the two should be conjugate is that C and D should be at the same potential, and if this condition be satisfied there will never be any tendency for a current to flow along CD; the currents in the rest of the circuit will, therefore, not depend on CD.

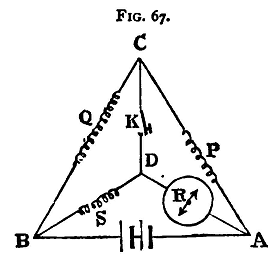
Suppose, now, a galvanometer is placed in the branch DA, and a key in CD (fig. 67), there will be a deflexion produced in the galvanometer. Adjust the resistance S until the galvanometer deflexion is unaltered by making or breaking contact in the branch CD. When this is the case it follows that AB and CD are conjugate, and, therefore, that

But R is the resistance of the galvanometer, which is thus measured by a null method without the use of a second galvanometer.

Fig. 68 shows the connections, using the Wheatstone-bridge box. A considerable portion of the current from the battery flows through the galvanometer, and the needle is thereby deflected. If a Thomson's galvanometer be used in the ordinary manner, the spot of light will be quite off the scale. In order to ascertain if the adjustment of the resistances is correct the mirror must be brought back to near its zero position by the aid of permanent magnets; it is probable that the control magnet will be too weak to do this alone, and others must be employed in addition. This constitutes one of the defects of the method; the field of magnetic force in which the needle hangs thus becomes very strong, and the sensitiveness of the galvanometer is thus diminished. By using a very weak electromotive force we may dispense with the additional magnets; the control magnet itself may be sufficient. We may attain this end by shunting the battery with a German-silver wire. The resistance suitable will depend on many conditions, and must be found by trial. A more economical method of diminishing the electromotive force between the points A and B is to introduce resistance into the battery circuit between point A or B and the pole. By making this interpolated resistance sufficiently great we may make the E.M.F. between A and B, what fraction we please of the total E.M.F. of the battery. And by increasing the resistance of the circuit we diminish the current which flows, and therefore diminish the consumption of zinc in the battery, whereas if the E.M.F. between A and B be reduced by shunting, the total current supplied by the battery is increased, and a larger expenditure of zinc is the result.

The battery used should be one of fairly constant E.M.F., for, if not, the current through the galvanometer will vary, and it will be difficult to make the necessary observations.

The method of proceeding is the same as that employed in the last section; the arms p and Q are first made equal, and two values found, differing by one ohm, between which S lies. The ratio P/Q is then made 0.1, and the first decimal place in the value of R obtained, and so on.

Experiment. - Determine, by Thomson's method, the resistance of the given galvanometer.

Enter result thus:

Galvanometer No. 6
Resistance 66.3 ohms.