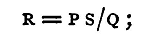Measurement of a Battery Resistance - Mance's Method

If we recollect that electromotive forces can be superposed, and that the resultant effect is simply the sum of the individual effects produced by each, it is clear that the condition that two conductors in a Wheatstone bridge, such as AB and CD (fig. 66), may be conjugate is not altered by the introduction of a second battery into any of the arms of the bridge. Such a battery will of course send a current through the galvanometer, and produce a deflexion, which will be superposed on that due to the battery in AB. Let a battery be put in the arm AD (fig. 69), R being its resistance, and let the galvanometer needle be brought back to its zero position by the use of external magnets. Adjust the resistance S until making or breaking contact in the battery circuit AB produces no effect on the galvanometer; that is, until the circuits AB and CD are conjugate. When this is the case we have

and P, S, and Q being known, we can find R, the resistance of the battery.

There is, however, no need for a second battery in AB; for the effect on the galvanometer due to this battery is zero when the conjugate condition is satisfied, whatever be its E.M.F. Take then the case when the E.M.F. is zero, i.e. connect A and B directly through a conductor. If the conjugate condition be satisfied this will produce no effect on the galvanometer; the deflexion due to the battery in AD will not be altered.

Again take the case in which the E.M.F. produced between A and B by the battery in AB is exactly equal and opposite to that produced between those points by the battery in AD. The galvanometer deflexion will still, if the conjugate condition hold, be unaltered. But in this case no current flows along AB; the conditions are the same as if A and B were insulated.

Thus the battery in AB may be supposed removed and replaced by a key. If the resistance s be adjusted until no effect is produced on the galvanometer by making contact with this key, it follows that the conjugate condition holds, and therefore R = PS/Q, so that R is determined. This is the principle of Mance's method.

Fig. 69 gives a diagram of the arrangement. Fig. 70 shows how the connections are made with the Wheatstone-bridge box.

The method of procedure is as follows: Make the arms P and Q equal. Make contact in the battery circuit with the key K'. Since any resistance which may exist in this key will of necessity be included in the measurement of the resistance R, it is important that its resistance should be small enough to be neglected. It is advisable to have a key in the circuit, for, as we have said already, it is always best to allow the current to flow through the coils only when actually required for the experiment.

Bring the spot of light back to the centre of the scale by the use of the control magnet and, if requisite by shunting the galvanometer.

Determine thus two values of S differing by 1 ohm, between which R lies. It must be remembered that any variation in S alters the permanent current through the galvanometer, and therefore the control magnet may require readjustment each time S is changed.

Make the ratio P/Q 0.1 and proceed in the same way to find the first decimal place in the value of R. Then make the ratio 0.01 and find a second decimal.

One difficulty requires special notice. It is true that making or breaking contact in the circuit AB will, if the conjugate condition hold, have no direct effect on the current in CD. It does, however, alter the total amount of current which is being produced by the battery. When AD is closed an additional circuit is open for this current; now with most batteries the E.M.F. depends somewhat on the current which the battery is producing, that is, on the rate at which chemical changes are going on in it; so that when the battery is called upon to do more work by the closing of the circuit AB, its E.M.F. is gradually altered and the permanent deflexion is thereby changed. On making contact with the key the spot of light may move, not because the conjugate condition is not satisfied, but because of this change in the E.M.F. of the battery. This is a fundamental defect in the method, and prevents the attainment of results of the highest accuracy. The difficulty may be partially obviated as follows:

It will be found that the displacement produced through the conjugate condition not being satisfied is a somewhat sudden jerk, while that which arises from variation in the E.M.F. is more gradual in its nature. A little practice is all that is required to recognise the difference between the two. Now it will always be possible to arrange the resistances so that the two displacements are in opposite directions. Let us suppose that it is found that when s is too large on making contact the jerk is to the right; the gradual deflexion to the left. Gradually decrease s until the jerk appears to be zero, and the spot seems to move steadily to the left, and take the value of s thus found as the one required. The results thus obtained will be found fairly consistent.

A more exact method for overcoming the difficulty, due to Professor O. J. Lodge, was described by him in the 'Philosophical Magazine' of 1876. This, however, involves the use of a specially constructed key, and for an account of it the reader must be referred to the original paper.

Experiment. - Determine by Mance's method the resistance of the given battery.

Enter results thus:

Leclanché cell (a) ........ 1.21 ohm
Leclanché cell (b) ........ 1.09 ohm
Sawdust Daniell ........... 10.95 ohm
Cylinder Daniell .......... 0.58 ohm