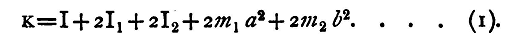Maxwell's Vibration Needle

The swinging body consists of a hollow cylindrical bar A B (fig. 14). Sliding in this are four equal tubes which together just fill up the length of the bar; two of these are empty, the other two are filled with lead.

CD is a brass piece screwed into the bar, and M is a plane mirror fastened to it with cement. At D is a screw, by means of which the bar is secured to the wire of which the modulus is required. E F is a horizontal scale placed so as to be reflected in the mirror M, and G H is a telescope adjusted to view the image of E F produced by the mirror. The eyepiece of the telescope is provided with cross-wires.

The first adjustment necessary is to arrange the apparatus so that when the bar is at rest the central division of the scale, which should be placed just above the telescope, appears, in the field of view of the telescope, to be nearly coincident with the vertical cross-wire. The mirror must be adjusted either by loosening the screw D and turning the bar round, or by turning the support which carries the wire, until when in the position of rest the plane of the mirror is very nearly at right angles to M G.

When this is done, reduce the bar as nearly as possible to rest, and point the telescope towards the mirror. For this purpose focus the telescope on the mirror, move h until the mirror is seen in the centre of the field, and then fix it with a clamp.

Alter the focus of the telescope so as to view an object at about the same distance behind the mirror as the scale is in front.

For the present this may be done quite roughly, by slightly pushing in the eye-piece.

If the scale happen to be in adjustment, the image will be seen in the mirror.

If this be not the case, move your head about behind the telescope until the scale is seen reflected in the mirror. Notice the position of your eye with reference to the telescope, and infer from this how the scale requires to be moved Thus, if your eye is above the telescope, the scale is too low, and vice versa.

Move the scale in the direction required until it is in the field of view of the telescope, and fix it securely.

There is another way of performing this adjustment, which may sometimes prove more rapid. Looking through the telescope, move a lighted lamp or match about until a glimpse of it is caught reflected in the mirror. The position of the lamp at that moment shows you where the scale should be.

(If the first method be adopted, it is easier to see the scale by going close up to the mirror until it comes into view, and then moving backwards to the telescope, still keeping it in sight.)

Suppose now the scale is seen reflected from the mirror; the central division of the scale will probably not coincide with the cross-wire.

For many purposes this is unimportant. If, however, we wish to bring the two together we must notice what point on the scale will come opposite the cross-wire when the mirror is at rest,⁽¹⁾ and then turn the torsion head, which carries the wire in the right direction until the central division is brought into view.

It may be impossible to make the adjustment in this manner; in that case we must move the telescope and scale.

Thus, if O be the central division of the scale and P the division which coincides with the cross-wire, the necessary adjustment will be made if we move the telescope and scale through half the distance OP, still keeping the former pointed to the mirror.

It is sometimes necessary to set the scale at right angles to M O or M G. For this purpose measure with a string or tape the distances of E M and F M, and turn the scale round a vertical axis until these two are equal. Then since O E = O F and M E = M F, it is clear that O M and E F are at right angles, and the required adjustments are complete.

To observe the Time of a Complete Vibration.

Twist the bar slightly from its position of rest, and let it vibrate.

The scale will appear to cross the field of view of the telescope.

Note with a watch or chronometer the instant at which the middle point of the scale passes the cross-wire of the telescope, marking also the direction in which the scale appears to be moving. Let us suppose it is from left to right. It is of course impossible to see at the same time the cross-wire and scale and also the face of the chronometer; but the observation may be effected either as described in the section on rating a watch or as follows.

Let us suppose the chronometer ticks half-seconds.

Listen carefully for the sound of the tick next after the transit of the central division of the scale, and count six in time with the ticks, moving at the same time the eye from the telescope to the clock-face. Suppose that at the sixth tick the chronometer registers 10 h. 25 min. 31.5 sec., then the instant of transit was 3 sec. earlier, or 10 h. 25 min. 28.5 sec. Raise the eye quickly back to the telescope and watch for the next transit from left to right.

Again count six ticks, moving the eye to the chronometer, and let the time be 10 h. 26 min. 22 sec.

The time of the second transit is then 10 h. 26 min. 19 sec., and the time of a complete vibration is 50.5 sec.

But either observation may be wrong by 0.5 sec., so that this result is only accurate to within 1 sec.

To obtain a more accurate result proceed exactly as in §20.

It may happen that the time of vibration is so short that we have not time to perform all the. necessary operations - namely, to move the eye from the telescope, look at the chronometer, note the result, and be ready for another transit before that transit occurs. In such a case we must observe every second or third transit instead of each one.

Again, we may find that 6 ticks do not give time to move the eye from the telescope to the chronometer-face. If this be so, we must take 8 or 10. Practice, however, soon renders the work more rapid.

Of course, if we always count the same number of ticks there is no need to subtract the 3 sec. from the chronometer reading; we are concerned only with the differences between the times of transit, and the 3 sec. affects all alike.

We may thus observe t₁ the time of vibration of the needle when the empty tubes are nearest the ends, the loaded tubes being in the middle; and in the same manner we may observe t₂ the time of vibration of the needle when the positions of the heavy and light tubes have been interchanged. Let the observed value of t₁ be 17.496 sec., and that of t₂, 25.263 sec.

To find the Value of k, the Increase in the Moment of Inertia.

We know that the moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of gravity, together with the moment of inertia of the whole mass collected at its centre of gravity about the given axis (p. 44).

Thus, let m be the mass of a body whose moment of inertia about a certain axis is I; let a be the distance of the centre of gravity from that axis, and /I the moment of inertia about a parallel axis through the centre of gravity.

Then I = /I + ma².

Moreover, the moment of inertia of a body is the sum of the moments of inertia of its parts (p. 44).

Now, let m₁ be the mass of each of the heavy tubes, and a the distance of the centre of each of them from the axis round which the whole is twisting when in the first position. Let I₁ be the moment of inertia of each of the heavy tubes about a parallel axis through its centre. Let m₂ I₂ have the same meaning for the empty tubes, and let b be the distance of the centre of each of these from the axis of rotation.

Let I be the moment of inertia of the empty case.

Then

In the second position, a is the distance from the axis of rotation of the centre of each of the masses m₂, b of that of the masses m₁.

To find the moment of inertia of the whole, therefore, we require simply to interchange a and b in equation (1), and this moment of inertia is K+k. Thus,

from (1) and (2) k=2(b² - a²)(m₁ - m₂).

Thus, we do not need to know I, I₁ or I₂ to find k. Now the length of each of the tubes is one-fourth of that of the whole bar A B. Calling this c, we have

and

To find m₁ and m₂ we require merely to determine by weighing the number of grammes which each contains. Our formula for τ (p. 146) becomes

and it only remains to measure l. This can be done by means of the beam compass or a measuring tape.

We must, of course, measure from the point at which the upper end of the wire is attached, to the point at which it is clipped by the screw D.

The wire it will be found fits into a socket at the top of the apparatus C D. Be careful when fixing it initially to push it as far as possible into the socket; its position can then be recovered at any time.

Unloose the screw D and draw the wire from above, up through the tube which supports it, and measure its length in the ordinary manner.

The value of τ thus obtained gives the modulus of torsion for the particular specimen of wire. If the modulus of torsion for the material is required, we must make use of the additional law of torsional elasticity that the torsional couple in wires of the same material, differing only in area of section, is proportional to the fourth power of the radius of the wire. To find the value of the modulus of torsion of the material, the value of r must be divided by πr⁴/2 where r is the radius in centimetres (p. 140).

Experiment - Determine the modulus of torsion of the given wire.

Enter results thus:

t1 = 5.95 s           t2 = 9.75 s
m1 = 351.25 g         m2 = 60.22 g
l = 57.16 cm          c = 45.55 cm
τ = 5.67*106

(1)	When the position on the scale of the 'turning-points' of the needle can be read through the telescope, the position of equilibrium can be determined in exactly the same manner as in the case of the balance.