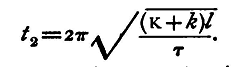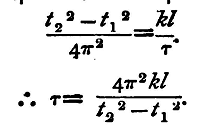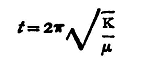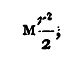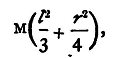Modulus of Torsion of a Wire

If the wire contain l units of length, and the end be twisted through a unit angle, each unit of length is twisted through an angle 1/l, and the couple required to do this is τ/l where τ is the modulus of torsion of the wire.

The couple required to twist unit length through an angle θ τθ, that required to twist a length l through an angle θ is τθ/l.

Suppose a mass, whose moment of inertia¹ is K, is fixed rigidly to the wire, which is then twisted, the mass will oscillate, and if t₁ sec. be the time of a complete oscillation, it can be shown that

To find τ, then, we require to measure t₁ and K.

K can be calculated if the body be one of certain determinate shapes.

If not, we may proceed thus: We can alter the moment of inertia of the system without altering the force tending to bring the body, when displaced, back to its position of equilibrium either (1) by suspending additional masses of known shape, whose moment of inertia about the axis of rotation can be calculated, or (2) by altering the configuration of the mass with reference to the axis of rotation. Suppose that in one of these two ways the moment of inertia is changed from K to K+k, where the change k in the moment of inertia can be calculated, although K cannot.

Observe the time of swing again. Let it be t₂.

Then

Thus

Whence

Thus τ can be expressed in terms of the observed quantities t₁, t₂ and l, and the quantity k which can be calculated.

We proceed to give the experimental details of the application of this method of finding the modulus of torsion of a wire by observing the times of vibration, t₁, t₂, when the moments of inertia of the suspended mass are K and K+k respectively. The change in the moment of inertia is produced on the plan numbered (2) above, by a very convenient piece of apparatus devised by Maxwell, and described in his paper on the Viscosity of Gases.

1

Moment of Inertia. - The moment of inertia of a body about a given axis may be defined physically as follows: If a body oscillates about an axis under the action of forces which when the body is displaced from its position of equilibrium through an angle θ, produce a couple tending to bring it back again, whose moment about the axis of rotation is μθ, then the time of a complete oscillation of the body about that axis will be given by the formula where K is a 'constant' which depends upon the mass and configuration of the oscillating body, and is called the moment of inertia of the body about the axis of rotation. It is shown in works on Rigid Dynamics that the relation between the moment of inertia K and the mass and configuration of the body is arrived at thus: K is equivalent to the sum of the products of every small elementary mass, into which the body may be supposed divided, into the square of its distance from the axis about which the moment of inertia is required, or in analytical language K = Σmr2 (Routh's 'Rigid Dynamics', chap. iii.). The following are the principal propositions which follow from this relation (Routh's 'Rigid Dynamics', chap, i.): (1) The moment of inertia of a body about any axis is equal to the sum of the moments of inertia of its separate parts about the same axis. (2) The moment of inertia of a body about any axis is equal to the moment of inertia of the body about a parallel axis through the centre of gravity together with the moment of inertia of a mass equal to the mass of the body supposed collected at its centre of gravity about the original axis. (3) The moment of inertia of a sphere of mass M and radius a about a diameter is 2Ma2/5. (4) The moment of inertia of a right solid parellelepiped, mass M, whose edges are 2a, 2b, 2c about an axis through its centre perpendicular to the plane containing the edges b and c is (5) The moment of inertia of a solid cylinder mass M and radius r about its axis of figure is about an axis through its centre perpendicular to the length of the cylinder, where 2l is the length of the cylinder. It is evident from the fact that in calculating the moment of inertia the mass of each element is multiplied by the square of its distance from the axis, the moment of inertia will in general be different for different disrributions of the same mass with reference to the axis.