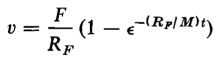Mass and Viscous Friction

Consider a constant force F applied horizontally to a body of constant mass M moving along a stationary horizontal surface. Assume that the force required to overcome the frictional resistance alone is proportional to the velocity of the body. Such an assumption is valid to a good degree of approximation in the case of lubricated surfaces, once the moving body has attained an appreciable velocity. Then

[1-29]

where R_Fv is the component of force required to overcome frictional resistance and M dv/dt is the component of force required to overcome the inertia of the body. The mechanical power input to this system is

as v and F are both in the same direction, the angle between these vectors thus being zero. Hence

[1-30]

In Eq. 1-30 the component of power represented by the term R_Fv² is the one converted into heat. The term Mv dv/dt represents the power expended in storing kinetic energy in the mass M. If v is constant, dv/dt = 0 and there is no energy storage because all of the power p is converted into heat. If dv/dt is positive the mass M undergoes acceleration and stores kinetic energy. On the other hand if dv/dt is negative the mass M decelerates and gives up its stored kinetic energy and the power R_Fv² being converted into heat is greater than the applied power p. The energy input into this system is expressed by

Further, if the body starts from rest, i.e., v = 0, when t = 0 under the influence of the constant force F we have

[1-31]

Mv²/2 represents the stored energy and represents the mechanical energy converted into thermal energy.

For this condition the solution of Eq. 1-29 expresses the velocity as a function of time as follows

[1-32]

Separation of the variables yields

from which

[1-33]

when t = 0, and v = 0, hence

and

[1-34]

Figure 1-6. Velocity of a mass moving against viscous resistance under constant applied force.

Equation 1-34 is plotted in Fig. 1-6 and shows the final value v = F/R_F to be an asymptote that is approached as the time t approaches infinity.

Time constant

The reciprocal of the constant R_F/M in the exponent of Eq. 1-34 is called the time constant τ. Hence

and Eq. 1-34 can be rewritten as

[1-35]

The time constant also expresses the time required for the velocity v to attain the asymptotic value F/R_F if the acceleration were maintained constant at its initial value. This is indicated in Fig. 1-6 by the tangent to the curve at t = 0.

Since the friction absorbs some of the applied energy in irreversible form, i.e., in the form of heat, the acceleration is not constant but decreases with time. Hence the velocity when t = τ sec is determined from Eq. 1-34 or 1-35 as follows

[1-36]

where F/R_F = the velocity as the time t approaches infinity.