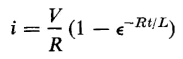Resistance and Self-Inductance

Figure 1-7 shows a schematic diagram of an R-L circuit. When there is current in such a circuit, the self-inductance has energy that is stored electro-magnetically. The electrical energy in the resistance is converted into thermal energy. The mathematical relationships in this kind of circuit are very similar to those in the mechanical system involving mass and friction.

Figure 1.7. R-L circuit.

In Fig. 1-7 the applied voltage V is constant and equals two components

[1-37]

e_R = i_R, the resistance drop
e_L = L di/dt, the emf of self-induction
R = resistance of the circuit in ohms
L = self-inductance of the circuit in henries and is constant
i = current in amperes
V = applied voltage in volts
t = time in seconds

Equation 1-37 can be rewritten as

and the power is expressed by

The electric power converted into heat is Ri² and that stored electro-magnetically is Li di/dt. The energy relationship is expressed by the following

[1-38]

If the initial conditions are i = 0 when t = 0, then Eq. 1-38 becomes

[1-39]

where Li²/2 represents the energy stored in the self-inductance. If the initial conditions are such that i = 0 when t = 0, the current in the R-L circuit is expressed by

[1-40]

The reciprocal L/R of the constant term in the exponent of Eq. 1-40 is the time constant t. It corresponds to the time constant M/R_F in the mechanical system.

Figure 1-8. Characteristics of an R-L series circuit with constant applied voltage.

A comparison of Eq. 1-34 with 1-40 shows that if voltage is taken as analogous to force and electrical resistance as analogous to frictional resistance in the mechanical system, current corresponds to velocity and self-inductance to inertia. Curves similar to those shown in Fig. 1-8 would portray the relationships for the mechanical system.

Thus the curve of current i vs time could be used to relate the velocity v to time in the mechanical system. Similarly, the curve of p_φ vs time could be used to represent the mechanical power Mv dv/dt, which stores energy in the moving mass of the mechanical system. The energy 1/2Mv² stored in the mass could also be represented as a function of time by the curve of W_L vs time.