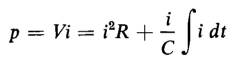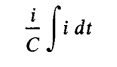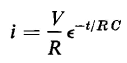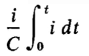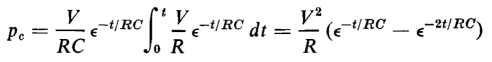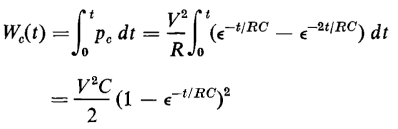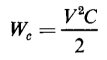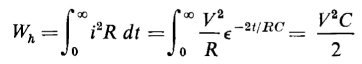Resistance and Capacitance

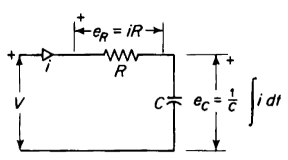
Figure 1-10 shows a circuit of capacitance in series with resistance. When a voltage is sustained across such a circuit the capacitance has energy that is stored electrostatically. The mathematical relationships in this kind of a circuit are quite similar to those in the mechanical system involving elasticity and friction. In Fig. 1-10 a constant voltage V is applied and

[1-50]

Figure 1-10. R-C circuit

and

[1-51]

is the expression for power.

The term i²R expresses the power that is converted into heat and the term

expresses the power that stores energy in the capacitance.

The solution of Eq. 1-51 for the condition that when t = 0 there is no energy stored in the capacitance, yields

[1-52]

In Eq. 1-51 the power that stores energy in the capacitance is expressed by the term

If Eq. 1-52 is substituted in this term, the result is

[1-53]

The energy stored in the capacitor at any time t after the constant voltage V is applied to the circuit is expressed by

[1-54]

The energy in the capacitance approaches its final value as t approaches infinity. Hence, from Eq. 1-54

[1-55]

The expression for the energy converted into heat is from Eq. 1-52

[1-56]

Equations 1-55 and 1-56 show that the energy converted into heat in the R-C circuit with constant applied voltage is equal to the energy stored in the capacitor as time increases without limit. In the case of the spring under constant applied force, the total energy converted into heat is also equal to the energy stored in the spring as time increases without limit.

Figure 1 - 11. Characteristics of an R-C series circuit with constant applied d-c voltage.

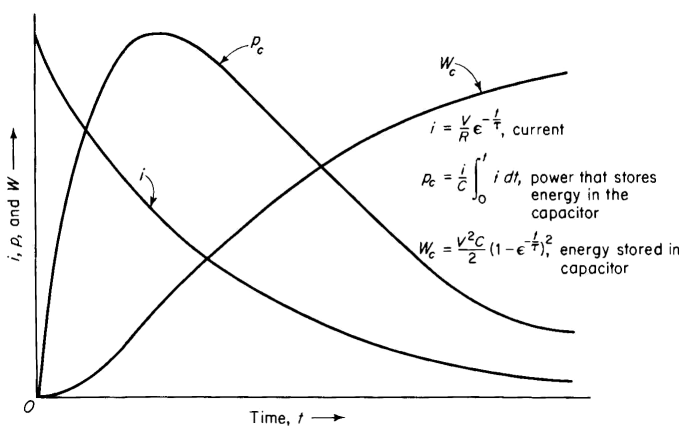
The variation with respect to time of current, power and, energy in the capacitor is shown graphically in Fig. 1-11. The same graph can be used to express the relationships for the massless spring. In that case the curve that shows the relationship between current and time in Fig. 1-11 would show the variation of the velocity of the force F in Fig. 1-9. Similarly the curve p_c in Fig. 1-11 would indicate the power that stores energy in the spring as a function of time, whereas the curve w_c would show the amount of energy stored in the spring as a function of time.

The time constant for the R-C circuit is τ = RC sec. Similarly the time constant for the mechanical system with the massless spring is τ = R_F/S sec.