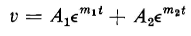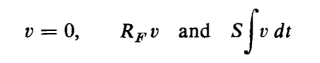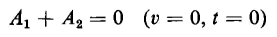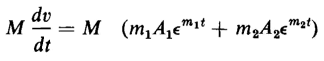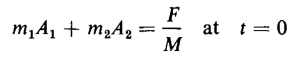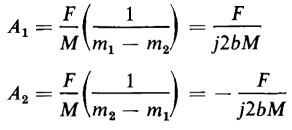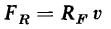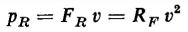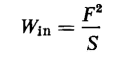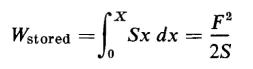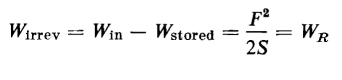| Capacitors, Magnetic Circuits, and Transformers is a free introductory textbook on the physics of capacitors, coils, and transformers. See the editorial for more information.... |

|

Home  Energy Energy  Spring, Mass, and Viscous Friction Spring, Mass, and Viscous Friction |
|||||||||||||||||||||||||||||||||||






|
|||||||||||||||||||||||||||||||||||
Spring, Mass, and Viscous Friction
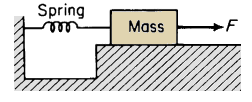
Figure 1-12 shows a system in which a spring is extended by applying a force F to the mass M starting from rest. Let v = the velocity at which the spring is extended, then
where RF = constant of viscous friction, newton seconds per meter
Differentiation of Eq. 1-57 with respect to time yields
The relationship
is a solution that satisfies Eq. 1-58 and upon substitution of Eq. 1-59 in Eq. 1-58 there results
Equation 1-60 divided by εmt yields
or
where j = Since Eq. 1-57 is a second order differential equation, two constants of integration are involved in the general solution, and the velocity is expressed by
To evaluate the constants of integration A1 and A2 let t = 0, Now at t = 0, v = 0 as the mass is started from rest. Furthermore, if
must both be zero at t = 0. Therefore
So
From Eqs. 1-63 and 1-65 we have
Substitution of Eq. 1-66 in Eq. 1-62 yields
Frictional losses The force required to overcome frictional resistance is
and the power converted into heat, i.e., heat expended in overcoming friction, is
The energy converted into heat through friction is
The same relationship can be derived in a simpler manner on the basis of Eq. 1-3. The gain in reversible energy is the energy stored in the spring, whereas the irreversible energy is in the form of heat, some of which raises the temperature of part of the system, thus representing a gain in irreversible energy; the remainder of the heat is dissipated to media surrounding the system. When Eq, 1-3 is applied to this case the following relationship is valid
Accordingly, for this situation Eq. 1-3 can be reduced to
where X = F/S so that the total energy input
The gain in reversible energy is the energy stored in the spring
Then from Eq. 1-72 the irreversible energy is
The final energy stored in the spring is also F2/2S. Hence the total energy input to the system is F2/S. One-half of this is converted into heat.
|
|||||||||||||||||||||||||||||||||||
Home  Energy Energy  Spring, Mass, and Viscous Friction Spring, Mass, and Viscous Friction |
|||||||||||||||||||||||||||||||||||
Last Update: 2011-01-12


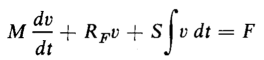
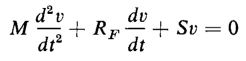
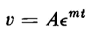
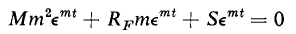
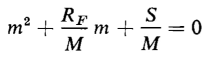
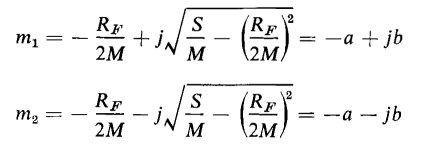
 .
.