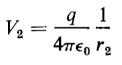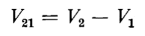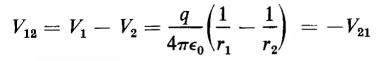Voltage and Potential

When the test charge q_t is moved in a direction toward the source charge, it is moved against the Coulomb force of repulsion and, energy is put into the system. On the other hand, if the test charge is moved in a direction

Figure 2-4. Projection of differential distance on force vector

away from the source charge, the system gives up energy and the energy input to the system is negative. Hence, in moving the test charge qt through a differential distance ds the differential energy input to the system is expressed by

[2-7]

where θ is the angle between the direction of the force and the direction of the differential distance ds as shown in Fig. 2-4.

The energy input to the system when the test charge is carried from a point P₁ at a distance r₁ from the source charge to a point P₂ at a distance r₂ from the source charge along any path whatsoever, as for example that illustrated in Fig. 2-5, is expressed by

[2-8]

From Fig, 2-4 it is evident that the scalar product i_rds is the projection of the differential distance vector ds upon r and is dr because in Eq. 2-7

Hence

[2-9]

Equation 2-9 divided by q_t yields

[2-10]

Equation 2-10 expresses the voltage between the points P₁ and P₂, the point P₂ being at a potential higher than that of P₁. The voltage V₂₁ is positive.

Figure 2-5. Difference of potential between two points

If the point P₁ in Fig. 2-5 were removed to an infinite distance then the voltage between the point P₂ and point P₁ would be expressed by

[2-11]

However, from Eq. 2-9 it is evident that the energy required to move the test charge from an infinite distance

[2-12]

because r₁ approaches infinity. The energy associated with the test charge at an infinite distance is zero. Hence, if Eq. 2-12 is divided by q_t, Eq. 2-11 results. Equation 2-11 expresses the potential of the point P₂. Similarly the potential of point P₁ is expressed by

[2-13]

If Eq. 2-13 is subtracted from Eq. 2-11 the result is the difference of potential between point P₂ and point P₁ and Eq. 2-10 is obtained. From this it follows that

[2-14]

Thus the voltage between the points P₁ and P₂ is simply the difference of electrical potential, the point P₂ being at a higher potential than P₁ This means also that the voltage V₂₁ is positive. Similarly the potential difference obtained by subtracting Eq. 2-11 from Eq. 2-13 results in

[2-15]

and V₁₂ is negative.

It is evident from Eq. 2-8 that the work done in carrying a test charge from one point to another in an electric field is independent of the path along which the charge is carried. By the same token if the test charge is carried from the second point back to the first along any path whatsoever, the same amount of energy is given up. Hence

[2-16]

This can also be expressed as a line integral as follows

from which

[2-17]

Equation 2-17 states that the summation of the electric field intensity around a closed path in an electrostatic field is zero.