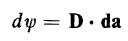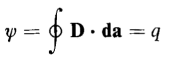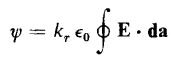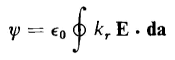Gauss's Theorem

Gauss's theorem states that the net electric flux emanating from an imaginary closed surface is equal to the net electric charge enclosed within that surface.

Figure 2-6. Gaussian surfaces

Thus in Fig. 2-6 the electric flux that emanates from surface (1) is equal to +q and that from surface (2) is equal to -q. The flux that emanates from surface (3) is zero because that surface does not enclose any charge. The flux that emanates from surface (4) is likewise zero because that surface encloses equal but opposite charges, the net charge being zero.

Figure 2-7. Flux density in differential area on a closed surface

Consider a differential area da of a closed surface, as shown in Fig. 2-7, with an electric flux density of D coulombs per square meter. The flux emanating from the surface represented by this differential area is expressed by

[2-18]

It must be kept in mind that the vector da, which represents the area of a surface, is normal to that surface. The product in Eq. 2-18 is a scalar product.

The scalar product of the infinitesimal area and the normal component of flux density integrated over the entire enclosing surface yields the total flux emanating from this surface, i.e.

[2-19]

This flux may also be expressed in terms of the surface integral of electric field intensity. If the enclosing surface lies completely within a medium having a fixed relative dielectric constant k_r, the relationship in Eq. 2-19 can also be expressed by

[2-20]

because

On the other hand, if the enclosing surface lies in a medium in which the relative dielectric constant k_r is not fixed, then the flux is expressed in terms of electric field intensity by

[2-21]

An example of a variation in k_r is the case of a medium in which k_r is a function of the electric field intensity E. Another is one in which the enclosing surface might be partly in air, partly in oil, and partly in porcelain. Equations 2-19, 2-20, and 2-21 are valid regardless of the medium within the enclosing surface.